2015年第六届蓝桥杯省赛-I. 垒骰子

原题链接

题面

赌圣 atm 晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。

经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！

我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。

假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。

atm 想计算一下有多少种不同的可能的垒骰子方式。

两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。

由于方案数可能过多，请输出模 10⁹ + 7 的结果。

不要小看了 atm 的骰子数量哦～

输入描述

输入第一行两个整数 n,m，n 表示骰子数目；

接下来 m 行，每行两个整数 a,b，表示 a 和 b 数字不能紧贴在一起。

其中，$0 < n \leq 10^9, m \leq 36$。

输出描述

输出一行一个数，表示答案模 10⁹+7 的结果。

输入样例

2 1
1 2

输出样例

544

题解

矩阵快速幂，动态规划

从下到上一层一层的垒骰子，对于样例，1 和 2 不能接触，则以 4 为顶（1位底）的其下面一层不能以 2 为顶，以 5 为顶（2位底）的其下面一层不能以 1 为顶，记 f[i][j] 表示当前摆了 i 层骰子，且第 i 层的骰子以 j 为顶的方案数，则对于第一层：

$f[1][1] = 4 \\ f[1][2] = 4 \\ f[1][3] = 4 \\ f[1][4] = 4 \\ f[i][5] = 4 \\ f[i][6] = 4$

即第一层的每个数字为顶都有 4 种方案（因为除开顶面和底面，可以旋转 4 次，使侧面的数字不同），则摆一层总共有 24 总方案。

对于第二层：

$f[2][1] = 4\times (f[1][1] + f[1][2] + f[1][3] + f[1][4] + f[1][5] + f[1][6]) \\ f[2][2] = 4\times (f[1][1] + f[1][2] + f[1][3] + f[1][4] + f[1][5] + f[1][6]) \\ f[2][3] = 4\times (f[1][1] + f[1][2] + f[1][3] + f[1][4] + f[1][5] + f[1][6]) \\ f[2][4] = 4\times (f[1][1] + f[1][3] + f[1][4] + f[1][5] + f[1][6]) \\ f[2][5] = 4\times (f[1][2] + f[1][3] + f[1][4] + f[1][5] + f[1][6]) \\ f[2][6] = 4\times (f[1][1] + f[1][2] + f[1][3] + f[1][4] + f[1][5] + f[1][6])$

其中第二层以 4 为顶的 f[2][4] 的底面为 1，则其下面一层不能以 2 为顶，同理 f[2][5] 的底面为 1，下一层不能以 2 为顶，所以不用加上他们。乘 4 是因为当前固定最上层顶面的情况下，旋转侧面4次得到不同的4种方案。最终可以知道，摆两层共有 544 中方案。

则可以推导出下图面的矩阵乘法：

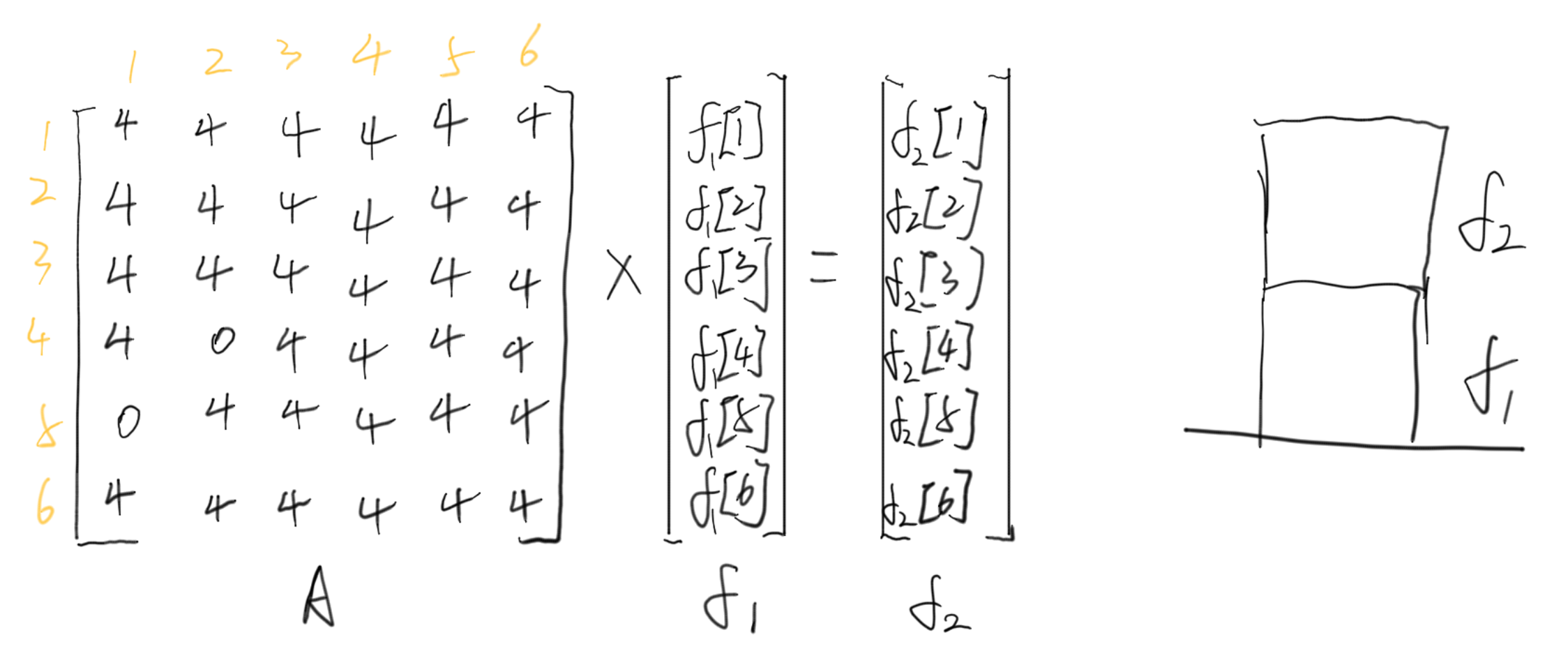
（上图中，A[i][j] 表示上层以数字 i 为顶，下层以数字 j 为顶的方案种类数。因为 1 和 2 不相贴，所以上层以 4 为顶时其底为 1， 则下层顶部不能为 2，则 $A[4][2] = 0$，同理 $A[5][1] = 0$。f₁[i] 代表第 1 层以 i 为顶的方案数，f₂[i] 代表第 2 层以 i 为顶的方案数）

可以看出，由 f₁ 计算出 f₂ 只需要在 f₁ 左乘上一个系数矩阵A即可，而该矩阵是由两个面能否接触决定的，是已知的，则由此可以进行如下递推：

$A\times f_1 = f_2 \\ A\times A\times f_1 = A\times f_2 = f_3 \\ A\times A\times A\times f_1 = A\times A\times f_2 = A\times f_3 = f_4 \\ \cdots \\ A^{n - 1} f_1 = f_n$

则可以知道摆放 n 层时，不同顶部数字的对应方案数，则本题需要用到矩阵的乘法运算，但此题 n 较大，最大可能有 10⁹， 直接一层循环去累乘矩阵需要进行 10⁹ 次的矩阵乘法运算，肯定会超时。我们可以利用和 快速幂 相同的思路，改写为矩阵快速幂，以便在进行 $\log_2^n$ 次矩阵乘法运算即可得出答案。

先将 $A^{n-1}$ 求出来后，再乘上第一层的6种基本方案数，则可以得到 n 层的不同顶部数字的方案数，再累加这6中不同顶部方案，可以得到最终的答案。

此题时间复杂度为 $O(6^3 \times log_2^n)$，最坏情况下计算约 7000 次，完全能解决本题。具体详见代码。

代码

#include<bits/stdc++.h>

using namespace std;

const int MOD = 1e9 + 7, M = 7;
int p[M] = {0, 4, 5, 6, 1, 2, 3}; //p[i] 表示数字 i 的对应面的数字
int n, m;

struct Matrix {
    int v[M][M];

    Matrix() {
        memset(v, 0, sizeof v);
    }

    void init() {    //置为单位矩阵
        for (int i = 1; i <= 6; i++) v[i][i] = 1;
    }

    Matrix operator*(const Matrix &b) {    //重载矩阵的乘法运算
        Matrix ans;
        for (int i = 1; i <= 6; i++) {
            for (int j = 1; j <= 6; j++) {
                int s = 0;
                for (int k = 1; k <= 6; k++) {
                    s = (s + v[i][k] * 1ll * b.v[k][j]) % MOD;
                }
                ans.v[i][j] = s;
            }
        }
        return ans;
    }
};

//矩阵快速幂
Matrix qpow(Matrix a, int n) {
    Matrix s;
    s.init();
    while (n) {
        if (n & 1) s = s * a;
        a = a * a;
        n >>= 1;
    }
    return s;
}

int main() {
    cin >> n >> m;
    Matrix a, x;
    for (int i = 1; i <= 6; i++) {
        x.v[i][1] = 4;  //第一层的每个数字为顶都有 4 中方案。
        for (int j = 1; j <= 6; j++) a.v[i][j] = 4; //将系数矩阵 a 全置为 4
    }
    for (int i = 0, x, y; i < m; i++) {
        scanf("%d%d", &x, &y);
        a.v[p[x]][y] = a.v[p[y]][x] = 0;
        //不能 x 和 y 不能接触，
        //   则以 x 为底的（以p[x]为顶）其下面一层不能以 y 为顶
        //   同理，以 y 为底的（以p[y]为顶）其下面一层不能以 x 为顶
    }

    Matrix b = qpow(a, n - 1) * x;
    int ans = 0;
    //累加 n 层6种不同顶部的方案数即为最终结果
    for (int i = 1; i <= 6; i++) ans = (ans + b.v[i][1]) % MOD;
    cout << ans << endl;

    return 0;
}