1 单源最短路径
1.1 Dijkstra算法
只能计算非负权值,时间复杂度 ,模板如下:
#include<iostream>
#include<cstring>
using namespace std;
const int N = 3010; //最大节点数
int a[N][N], d[N], n, m; // n 个节点, m条边
bool v[N];
void dijkstra() {
memset(d, 0x3f, sizeof(d));
memset(v, false, sizeof(v));
d[1] = 0;
for (int i = 1; i < n; i++) { //走 n-1 次,到达终点
int x = 0;
//找到未标记节点中 dist 最小的
for (int j = 1; j <= n; j++) {
if (!v[j] && (x == 0 || d[j] < d[x])) x = j;
}
v[x] = true;
//用全局最小值点 x 更新其他节点
for (int y = 1; y <= n; y++) d[y] = min(d[y], d[x] + a[x][y]);
}
}
int main() {
cin >> n >> m;
memset(a, 0x3f, sizeof(a));
for (int i = 1; i <= n; i++) a[i][i] = 0;
for (int i = 1; i <= m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
a[x][y] = min(a[x][y], z);
}
dijkstra();
for (int i = 1; i <= n; i++) cout << d[i] << " ";
puts("");
return 0;
}
1.2 Dijkstra算法(优先队列)
优先队列优化版本,复杂度
#include<iostream>
#include<cstring>
#include<queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e5 + 10, M = 1e6 + 10;
int head[N], ver[M], edge[M], Next[M], d[N];
bool v[N];
int n, m, tot;
void add(int x, int y, int z) {
ver[++tot] = y;
edge[tot] = z;
Next[tot] = head[x];
head[x] = tot;
}
void dijkstra() {
memset(d, 0x3f, sizeof d);
memset(v, false, sizeof v);
d[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> q; //小根堆
q.push(make_pair(0, 1));
while (q.size()) {
int x = q.top().second;
q.pop();
if (v[x]) continue;
v[x] = true;
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i], z = edge[i];
if (d[y] > d[x] + z) {
d[y] = d[x] + z;
q.push(make_pair(d[y], y));
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 1; i <= m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
}
dijkstra();
for (int i = 1; i <= n; i++) printf("%d ", d[i]);
puts("");
return 0;
}
1.3 Bellman-Ford算法
可以计算负权。常用于限制走几条边的最短路问题。时间复杂度 。
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 510, M = 10010;
int n, m, k;
int d[N];
int last[N];
struct Edge {
int a, b, c;
} edges[M];
void bellman_ford() {
memset(d, 0x3f, sizeof d);
d[1] = 0;
for (int i = 0; i < k; i++) {
memcpy(last, d, sizeof d);
for (int j = 0; j < m; j++) {
auto e = edges[j];
d[e.b] = min(d[e.b], last[e.a] + e.c);
}
}
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 0; i < m; i++) {
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edges[i] = {a, b, c};
}
bellman_ford();
if (d[n] > 0x3f3f3f3f / 2) puts("impossible");
else printf("%d\n", d[n]);
return 0;
}
1.4 Spfa算法
可计算负权,平均时间复杂度为,最坏时间复杂度 。
#include<iostream>
#include<cstring>
#include<cstdio>
#include<queue>
using namespace std;
const int N = 100010, M = 1000010;
int head[N], ver[M], Next[M], edge[M], d[N];
bool v[N];
int n, m, tot;
queue<int> q;
void add(int x, int y, int z) {
ver[++tot] = y;
edge[tot] = z;
Next[tot] = head[x];
head[x] = tot;
}
void spfa() {
memset(v, false, sizeof(v));
memset(d, 0x3f, sizeof(d)); //是否在队列中
d[1] = 0;
v[1] = true;
q.push(1);
while (q.size()) {
//取出队头
int x = q.front();
q.pop();
v[x] = false; //节点 x 已经不在队列了
//扫描所有出边
for (int i = head[x]; i; i = Next[i]) {
int y = ver[i], z = edge[i];
if (d[y] > d[x] + z) {
//更新,把新的二元组插入堆
d[y] = d[x] + z;
if (!v[y]) q.push(y), v[y] = true;
}
}
}
}
int main() {
cin >> n >> m;
for (int i = 0; i < m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
}
spfa();
for (int i = 1; i <= n; i++) cout << d[i] << " ";
puts("");
return 0;
}
2 任意两点间的最短距离
Floyd 算法
基于动态规划的思想,时间复杂度 。
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
const int N = 310;
int d[N][N], n, m;
int main() {
memset(d, 0x3f, sizeof(d));
cin >> n >> m;
for (int i = 1; i <= n; i++) d[i][i] = 0;
for (int i = 1; i <= m; i++) {
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
d[x][y] = min(d[x][y], z);
}
//floyd 求任意两点间的最短路径
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
//结果输出
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cout << d[i][j] << " ";
}
puts("");
}
return 0;
}
3 最小生成树
3.1 Kruskal 算法
时间复杂度
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5, M = 2e5 + 5;
struct Edge {
int x, y, z;
bool operator<(const Edge &b) { //重载比较运算,较小的边优先级高
return z < b.z;
}
};
int m, n, fa[N];
Edge edge[M];
//并査集
int find(int x) {
if (x == fa[x]) return x;
return fa[x] = find(fa[x]);
}
int main() {
cin >> n >> m;
for (int i = 1, x, y, z; i <= m; i++) {
scanf("%d%d%d", &x, &y, &z);
edge[i] = {x, y, z};
}
//初始化并査集
for (int i = 1; i <= n; i++) fa[i] = i;
//对边集排序,权值小的边优先级高
sort(edge + 1, edge + m + 1);
int ans = 0, cnt = 0;
for (int i = 1; i <= m; i++) {
int x = find(edge[i].x);
int y = find(edge[i].y);
if (x == y) continue; //若两个顶点在同一集合,则不使用该条边
cnt++; //边数++
fa[x] = y; //将两点所在集合合并为同一集合
ans += edge[i].z; //最小生成树的权增加
}
if (cnt == n - 1) cout << ans << endl; //边数为顶点数量减一,则为最小生成树
else puts("impossible"); //不为最小生成树
return 0;
}
3.2 Prim 算法
主要用于稠密图,尤其是完全图的最小生成树求解。时间复杂度 。
#include<bits/stdc++.h>
using namespace std;
const int N = 510, INF = 0x3f3f3f3f;
int a[N][N], d[N];
bool v[N];
int n, m;
int prim() {
int ans = 0;
memset(d, 0x3f, sizeof d);
memset(v, false, sizeof v);
for (int i = 1; i <= n; i++) {
int x = 0;
for (int j = 1; j <= n; j++) { //找到还未访问过的从当前集合的节点中能到达的最近节点
if (!v[j] && (x == 0 || d[j] < d[x])) x = j;
}
if (x > 1 && d[x] == INF) return INF; //非第一个节点到当前集合的距离若为无穷,则说明至少有两个连通分量,则不存在最小生成树
if (x > 1) ans += d[x]; //非第一个进入集合需要加上边权
v[x] = true; //访问过的标记
for (int j = 1; j <= n; j++) { //更新当前集合所能到达的顶点的最短距离
d[j] = min(d[j], a[x][j]);
}
}
return ans;
}
int main() {
cin >> n >> m;
memset(a, 0x3f, sizeof a);
for (int i = 1; i <= n; i++) a[i][i] = 0;
for (int i = 0, x, y, z; i < m; i++) {
scanf("%d%d%d", &x, &y, &z);
a[x][y] = a[y][x] = min(a[x][y], z);
}
int res = prim();
if (res == INF) puts("impossible");
else cout << res << endl;
return 0;
}
4 负环判断
Spfa 算法
最坏时间复杂度
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int head[N], ver[N], edge[N], Next[N], tot;
int n, m;
int d[N], cnt[N];
bool v[N];
void add(int x, int y, int z){
ver[++tot] = y;
edge[tot] = z;
Next[tot] = head[x];
head[x] = tot;
}
bool spfa(){
queue<int> q;
for (int i = 1; i <= n; i ++ ){
v[i] = true;
q.push(i);
}
while(q.size()){
int x = q.front();
q.pop();
v[x] = false;
for(int i = head[x]; i; i = Next[i]){
int y = ver[i], z = edge[i];
if(d[y] > d[x] + z){
d[y] = d[x] + z;
cnt[y] = cnt[x] + 1;
if(cnt[y] >= n) return true;
if(!v[y]) {
q.push(y);
v[y] = true;
}
}
}
}
return false;
}
int main(){
cin >> n >> m;
for(int i = 1; i <= m; i++){
int x, y, z;
scanf("%d%d%d", &x, &y, &z);
add(x, y, z);
}
if(spfa()) puts("Yes");
else puts("No");
return 0;
}
5 拓扑排序
时间复杂度
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, m;
int head[N], Next[N], ver[N], tot, deg[N];
vector<int> ans; //保存拓扑序列答案
void add(int x, int y) {
ver[++tot] = y;
Next[tot] = head[x];
head[x] = tot;
}
void topSort() {
//广搜求拓扑序列
queue<int> q;
for (int i = 1; i <= n; i++) {
if (deg[i] == 0) q.push(i); //入度为0则入队
}
while (q.size()) {
auto now = q.front();
q.pop();
ans.push_back(now); //出队即进入答案序列
for (int i = head[now]; i; i = Next[i]) { //遍历当前节点的所有邻接节点
int y = ver[i];
if (--deg[y] == 0) q.push(y); //入度为0则入队
}
}
}
int main() {
cin >> n >> m;
for (int i = 1, x, y; i <= m; i++) {
scanf("%d%d", &x, &y);
add(x, y);
deg[y]++; //入度+1
}
topSort();
if (n == ans.size()) {
for (auto x:ans) printf("%d ", x);
puts("");
} else puts("-1"); //存在环,无拓扑序列
return 0;
}
6 最近公共祖先
- 距离:两点之间的距离
const int N = 1e4 + 5, M = 2e4 + 5, Deep = 14;
int head[N], ver[M], Next[M], edge[M], tot;
int depth[N], fa[N][Deep], dist[N][Deep];
int n, m;
void add(int x, int y, int z){
ver[++tot] = y;
edge[tot] = z;
Next[tot] = head[x];
head[x] = tot;
}
void bfs(){
memset(depth, 0x3f, sizeof depth);
depth[0] = 0;
depth[1] = 1;
queue<int> q;
q.push(1);
while(q.size()) {
int x = q.front();
q.pop();
for(int i = head[x]; i; i = Next[i]) {
int y = ver[i], z = edge[i];
if(depth[y] <= depth[x] + 1) continue; //访问过
depth[y] = depth[x] + 1;
q.push(y);
fa[y][0] = x;
dist[y][0] = z;
fir(k, 1, Deep - 1) {
fa[y][k] = fa[fa[y][k - 1]][k - 1];
dist[y][k] = dist[y][k - 1] + dist[fa[y][k - 1]][k - 1];
}
}
}
}
int lca(int x, int y){
int res = 0;
if(depth[x] < depth[y]) swap(x, y);
rif(k, Deep - 1, 0) {
if(depth[fa[x][k]] >= depth[y]) {
res += dist[x][k];
x = fa[x][k];
}
}
if(x == y) return res;
rif(k, Deep - 1, 0) {
if(fa[x][k] > 0 && fa[x][k] != fa[y][k]) {
res += dist[x][k] + dist[y][k];
x = fa[x][k];
y = fa[y][k];
}
}
res += dist[x][0] + dist[y][0];
return res;
}
7 图的相关定义

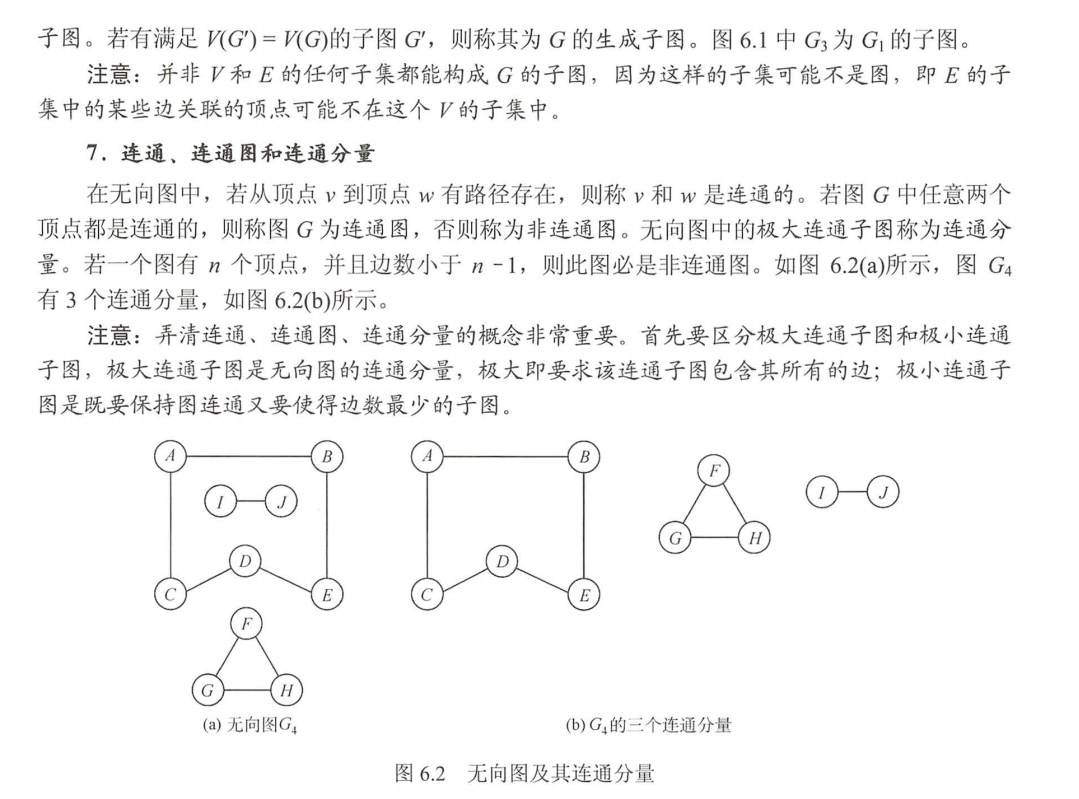
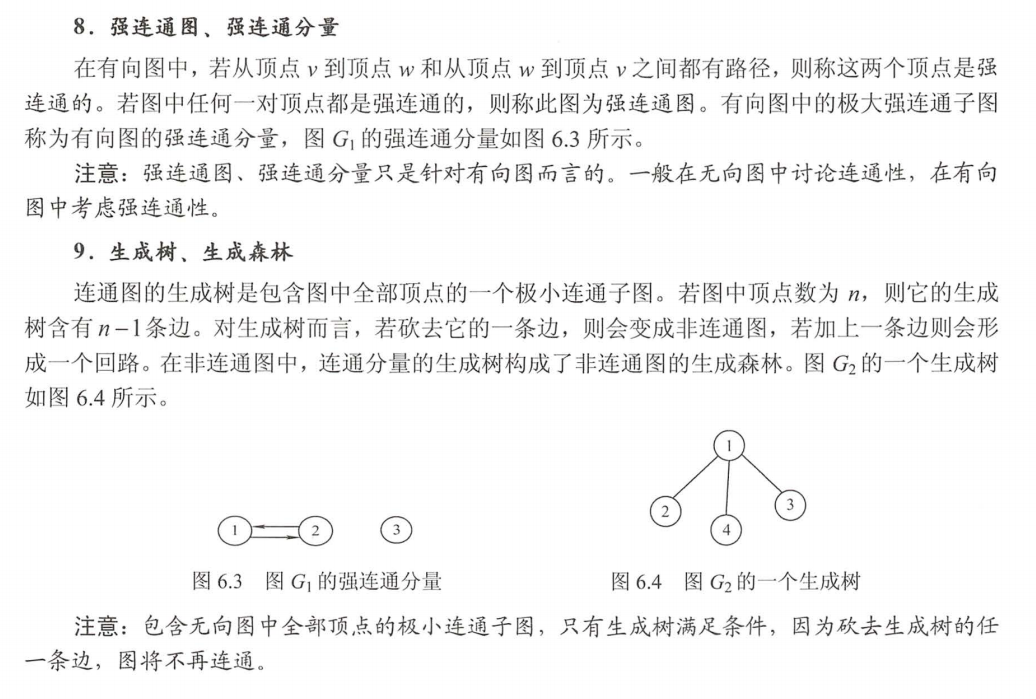


| 标题: | 信息学竞赛模板(十三)— 图论 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/82 |
| 更新: | 2023-03-13 09:06:05 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





