题面
【问题描述】
小蓝特别喜欢单调递增的事物。
在一个字符串中,如果取出若干个字符,将这些字符按照在字符串中的顺序排列后是单调递增的,则成为这个字符串中的一个单调递增子序列。
例如,在字符串 lanqiao 中,如果取出字符 n 和 q,则 nq 组成一个单调递增子序列。类似的单调递增子序列还有 lnq、i、ano 等等。
小蓝发现,有些子序列虽然位置不同,但是字符序列是一样的,例如取第 二个字符和最后一个字符可以取到 ao,取最后两个字符也可以取到 ao。小蓝 认为他们并没有本质不同。
对于一个字符串,小蓝想知道,本质不同的递增子序列有多少个?
例如,对于字符串 lanqiao,本质不同的递增子序列有 21 个。它们分别 是 l、a、n、q、i、o、ln、an、lq、aq、nq、ai、lo、ao、no、io、lnq、 anq、lno、ano、aio。
请问对于以下字符串(共 200 个小写英文字母,分四行显示):(如果你把 以下文字复制到文本文件中,请务必检查复制的内容是否与文档中的一致。在 试题目录下有一个文件 inc.txt,内容与下面的文本相同)
tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhf
iadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqij
gihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmad
vrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl
本质不同的递增子序列有多少个?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路
动态规划。分析如下图:
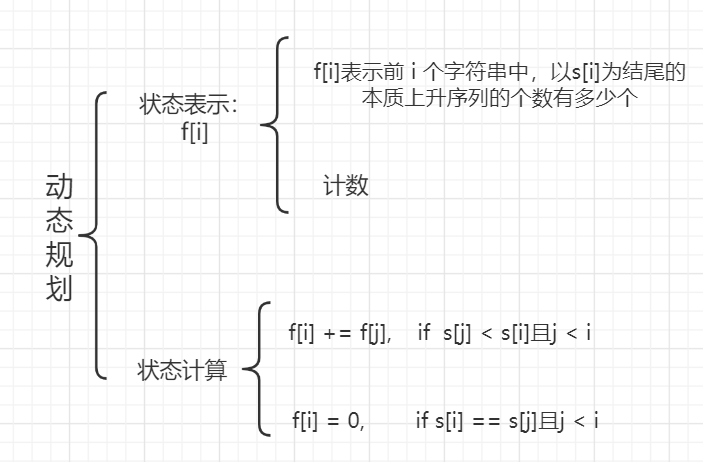
答案:3616159
代码
#include<iostream>
#include<string>
using namespace std;
const int N = 27;
int f[210];
int main() {
string str;
cin >> str;
int n = str.length();
for (int i = 1; i <= n; i++) {
f[i] = 1;
for (int j = 1; j < i; j++) {
if (str[i - 1] > str[j - 1]) f[i] += f[j];
if (str[i - 1] == str[j - 1]) f[i] = 0; //前面出现过一次,贡献清零
}
}
int res = 0;
for (int i = 1; i <= n; i++) {
res += f[i];
}
cout << res << endl;
return 0;
}
| 标题: | 2020第十一届蓝桥杯国赛-D本质上升序列 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/107 |
| 更新: | 2022-09-18 22:39:25 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





