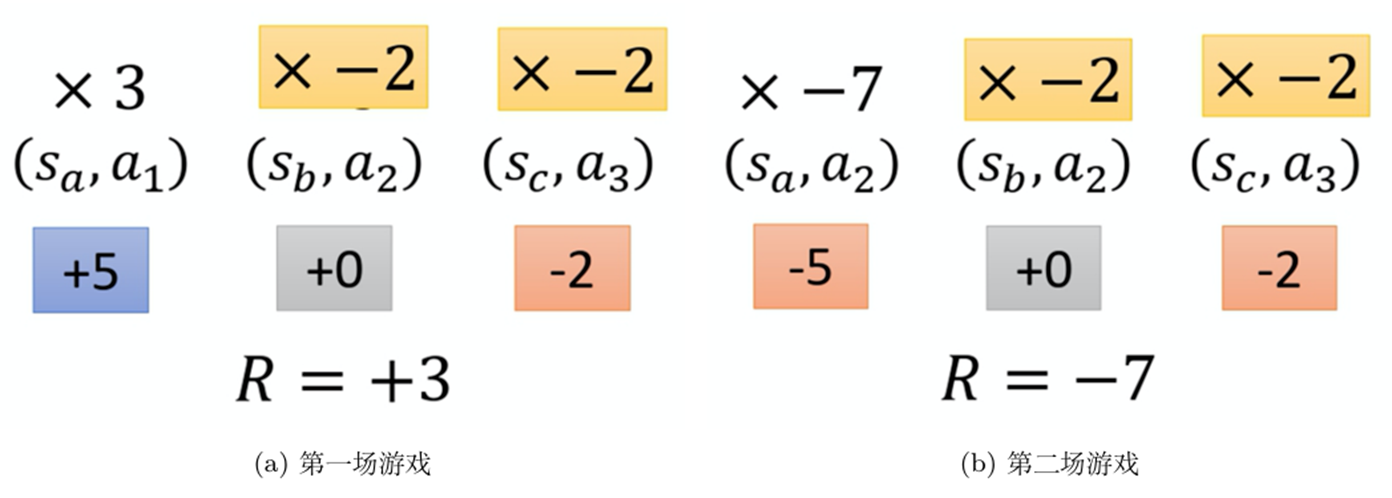策略梯度(Policy Gradient)

1 前言

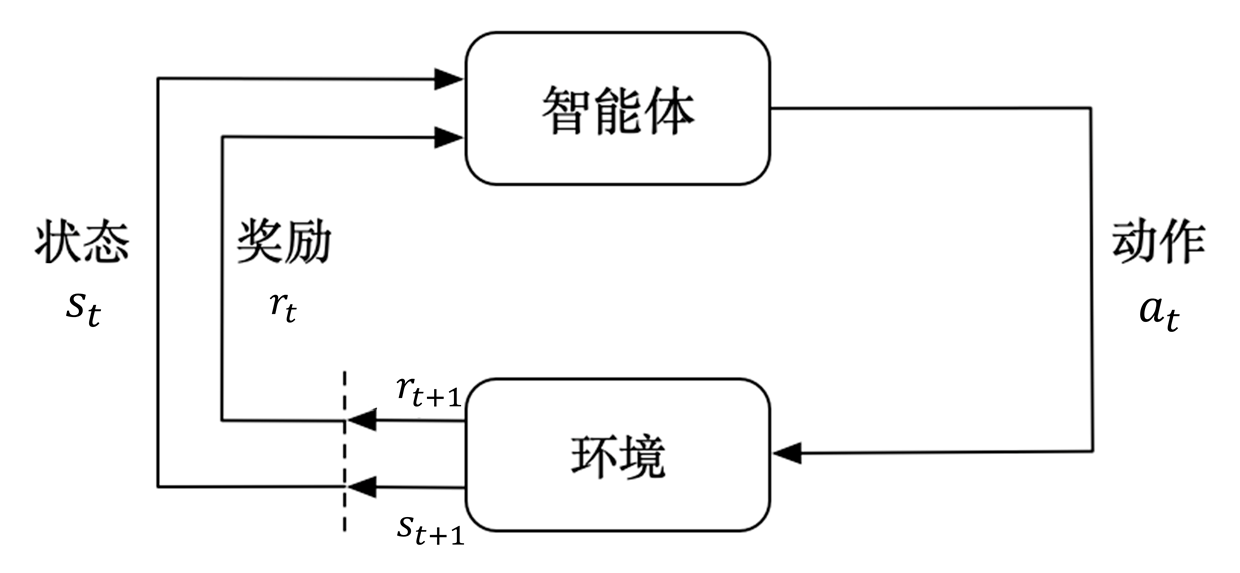
强化学习讨论的问题是智能体在与环境交互过程中，如何最大化其所获得的的累积奖励问题。即要求我们学习一个合适的策略，在面对不同的状态时做出最优的决策从而获得最大的奖励。如下图。

正如前面所介绍的，强化学习可以分为 Policy-Based 和 Value-Based。前者学习一个Actor根据其学习到的最优策略选择动作，而后者学习一个Value Function，通过贪心地选择使未来状态期望累积奖励最大的动作作为最优策略。更形象地说，前者相当于是一个学生，其通过书本以及课堂教学内容掌握了正确的解题方法和技巧，在考试的时候能在试卷上根据积累的知识填写出最优的答案，从而得到高分。而后者相当于是这个学生得到了试卷的标准答案，学生直接通过标准答案知道每个问题应该填写什么，他就写什么，从而也能得到高分。

即 Policy-based 是智能体自己内部决策应该怎么采取动作，而 Value-based 是智能体根据外部的价值函数来评估每个动作的好坏来选择动作。

接下来介绍一个 Policy-based 的算法，策略梯度(Policy Gradient, PG)。

2 Policy Gradient

2.1 策略梯度介绍

策略梯度算法是一类强化学习算法，其主要思想是通过对策略参数的优化来最大化长期回报的期望。在策略梯度算法中，通常采用概率分布函数表示策略，并通过最大化回报期望的方式来更新策略参数。

具体来说，设策略参数为$\theta$ ，环境状态为$s$，动作为$a$，回报为$R$，则策略$\pi(a|s,\theta)$的概率分布函数表示为：

$\pi(a|s,\theta) = P(a|s,\theta)$

在实际应用中，策略梯度算法通常采用基于神经网络的策略函数近似来表示策略，并通过反向传播算法来计算策略梯度和更新策略参数。可以将要学习的策略 $\pi$ 当做一个神经网络，其参数为 $\theta$，输入状态 $s$ 后能够输出一个动作 $a$ （确定性策略）或得到可选动作的概率进行采样得到动作（随机策略）。

在策略梯度算法中，通常采用策略梯度定理来更新策略参数，即：

$\nabla_{\theta}\bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} \nabla_{\theta} \log \pi(a_t|s_t, \theta) R(\tau^n)$

其中，$\bar{R}_\theta$ 表示策略 $\pi(a|s,\theta)$ 的回报期望，$N$ 表示采样轨迹的数量，$T_n$ 表示第 $n$ 个轨迹的长度，$R(\tau^n) = r_1+r_2+r_3+\dots+r_{T_n-1}$表示第 $n$ 条轨迹 $\tau^n$ 的累积奖励（回报）。这里的 $\nabla_{\theta} \log \pi(a_t|s_t, \theta)$ 即为策略的梯度。

注意： 为了简化问题，这里的推导过程中只考虑折扣因子为1的情况，即 $\gamma=1$。

根据策略梯度定理，可以通过采样生成轨迹，计算轨迹上每个状态下采取动作的概率和累积回报，从而估计策略梯度，并通过梯度上升的方式来更新策略参数，使得期望回报最大化。

那上面的式子是如何得到的呢？接下来，我们便开始推导。

2.2 策略梯度原理

首先，我们采样到一条轨迹 $\tau=\{s_1,a_1,s_2,a_2,\dots,s_{n-1},a_{n-1},s_n\}$，每个状态执行动作执行后得到的奖励为 $r_1,r_2,\dots,r_{n-1}$ ，那么这条轨迹被采样到的概率可以表示为：

$\begin{aligned} p_\theta(\tau)&=p(s_1)p_\theta(a_1|s_1)p(s_2|s_1,a_1)\cdots p_\theta(a_{n-1}|s_{n-1})p(s_n|s_{n-1},a_{n-1})\\ &=p(s_1)\prod_{i=1}^{n-1}p_\theta(a_i|s_i)p(s_{i+1}|s_i,a_i) \end{aligned}$

上述式子中，$p_\theta(s_1)$ 代表环境初始化得到的状态 $s_1$ 的概率，由环境提供；$p(s_{i+1}|s_i,a_i)$ 表示在状态 $s_i$ 执行了动作 $a_i$ 后，环境转移到动作 $s_{i+1}$ 的概率，由环境决定；而 $p_\theta(a_i|s_i)$ 表示在状态 $s_i$ 执行动作 $a_i$ 的概率，这是由我们自己的策略提供的。

这条轨迹的总奖励为 $R(\tau) = \sum_{t=1}^{n-1}r_t$，其中每个 $r_t$ 都是一个随机变量的取值，则总奖励的期望值如下：

$\bar{R}_\theta = \mathbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)] = \sum_{\tau} p_\theta(\tau)R(\tau)$

显然，我们希望执行策略能得到的累积奖励的期望最大，则需要对 $\bar{R}_\theta$ 做梯度上升（类似损失函数），即通过以下公式对策略的参数 $\theta$ 进行优化（$\alpha$ 代表学习率），以得到更好的策略使期望累积奖励更大。

$\theta \leftarrow \theta+\alpha\nabla\bar{R}_\theta$

接下来我们求 $\bar{R}_\theta$ 的梯度（这里为了简写，认为 $\nabla$ 是关于 $\theta$ 的梯度）：

$\begin{aligned} \nabla\bar{R}_\theta &= \sum_{\tau}R(\tau)\nabla p_\theta(\tau)\\ &=\sum_{\tau}R(\tau)p_\theta(\tau)\frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}\\ &=\sum_{\tau}R(\tau)p_\theta(\tau)\nabla \log p_\theta(\tau)\\ &=\mathbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log p_\theta(\tau)]\\ &\approx \frac{1}{N}\sum_{n=1}^NR(\tau^n)\nabla\log p_\theta(\tau^n)\\ &=\frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n-1}R(\tau^n)\nabla\log p_\theta(a_t^n|s_t^n) \end{aligned}$

其中，第一个式子中我们直接将 $R(\tau)$ 认为一个与策略参数 $\theta$ 无关的常数，无需关于 $\theta$ 可导，这是因为由策略梯度定理，期望累积奖励的梯度是与轨迹的梯度成正比的（详见Sutton《强化学习》第十三章）。第二个式子在第一个的基础上，乘上了 $p_\theta(\tau)/p_\theta(\tau)$ 得到的。又因为式子 $(\nabla p_\theta(\tau))/p_\theta(\tau) = \nabla\log p_\theta(\tau)$ 成立，则等价于第三个式子。然后第四个式子由大数定律，只要采样足够多的轨迹 $\tau$ 就能通过无偏估计逼近期望，从而约等于第五个式子。最后，在第五个式子中对于轨迹出现概率的梯度 $\nabla\log p_\theta(\tau^n)$ 有下式成立，则可以等于第六个式子。

$\begin{aligned} \nabla\log p_\theta(\tau^n) &=\nabla \log\left[ p(s_1^n)\prod_{t=1}^{T_n-1}p_\theta(a_t^n|s_t^n)p(s_{t+1}^n|s_t^n,a_t^n)\right] \\ &=\nabla\left[\log p(s_1^n) + \sum_{t=1}^{T_n-1}\log p_\theta(a_t^n|s_t^n) + \sum_{t=1}^{T_n-1}\log p(s_{t+1}^n|s_t^n,a_t^n)\right] \\ &=\nabla\log p(s_1^n) + \sum_{t=1}^{T_n-1}\nabla\log p_\theta(a_t^n|s_t^n) + \sum_{t=1}^{T_n-1}\nabla\log p(s_{t+1}^n|s_t^n,a_t^n) \\ &=\sum_{t=1}^{T_n-1}\nabla\log p_\theta(a_t^n|s_t^n) \end{aligned}$

上式中第三行到第四行，由于 $p(s_1^n)$ 和 $p(s_{t+1}^n|s_t^n,a_t^n)$ 是由环境提供的，其不包含策略的参数 $\theta$， 则其关于 $\theta$ 的梯度为$0$，则可得到第四行的结果。

综上，便可以得到最终的优化目标：

$\nabla\bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} R(\tau^n)\nabla \log p_\theta(a_t^n|s_t^n)$

$\theta \leftarrow \theta+\alpha\nabla\bar{R}_\theta$

2.3 直观理解策略梯度

$\begin{aligned} \nabla\bar{R}_\theta &\approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} R(\tau^n)\nabla \log p_\theta(a_t^n|s_t^n)\\ & = \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} R(\tau^n)\frac{\nabla p_\theta(a_t^n|s_t^n)}{p_\theta(a_t^n|s_t^n)} \end{aligned}$

观察上式，可以看到，参数 $\theta$ 的更新与 $R(\tau^n)$ 成正相关，与 $p_\theta(a_t^n|s_t^n)$ 成反比，前者使向着产生高回报的动作方向更新（如下图）；后者避免被选的高频非最优动作持续地增大被选概率，影响最优结果。

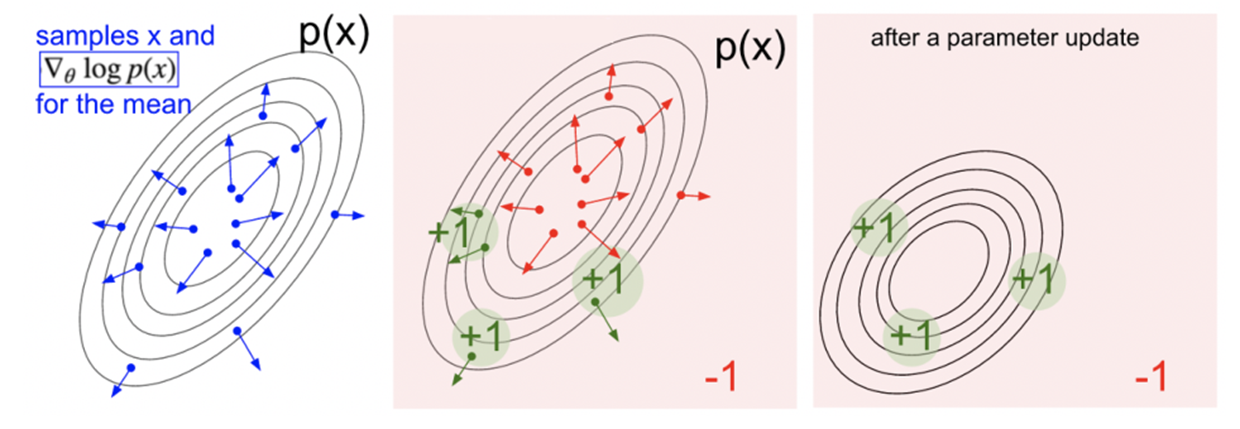
即可以理解为：增大带来正奖励的轨迹出现的概率；减小带来负奖励的轨迹出现的概率。

3 解决大方差问题

前面提到的 Policy Gradient 算法的方差很大，主要原因是它依赖于蒙特卡洛采样来估计回报的期望，而回报的估计涉及到对多条轨迹进行采样和求平均的过程，不同轨迹的回报差异较大，从而引入较大的方差。

解决方案：

1. 利用时间的因果关系
2. 添加基线（baseline）
3. 使用时序差分方法(Actor-Critic)

接下来我们具体来看看如何解决这个问题的。

3.1 利用时间的因果关系

PG算法只要在同一个回合里面，在同一场游戏里面，所有的状态-动作对就使用同样的奖励项进行加权。显然是不公平的，因为在同一场游戏里面，也许有些动作是好的，有些动作是不好的。

例如下图中第一条轨迹中总奖励为+3，则由上述更新公式，该条轨迹中出现的所有状态-动作对的概率都会上升，但实际上，该条中的一些状态-动作对并不都是能够带来正奖励的，如第三步的奖励就是-2，这个状态-动作对就不一定是好的，是由于第一步得到的高奖励消除了第三步的负奖励使整个轨迹的总奖励为正，让它出现的概率上升也不一定是一个好的优化。同理，第二条轨迹中第二步由于回合总奖励是-7，其状态-动作对出现概率会降低，但实际上其执行之后得到的后续回报为-2，其概率降低的程度应该比第一步的状态-动作对降低的程度低，才合理。

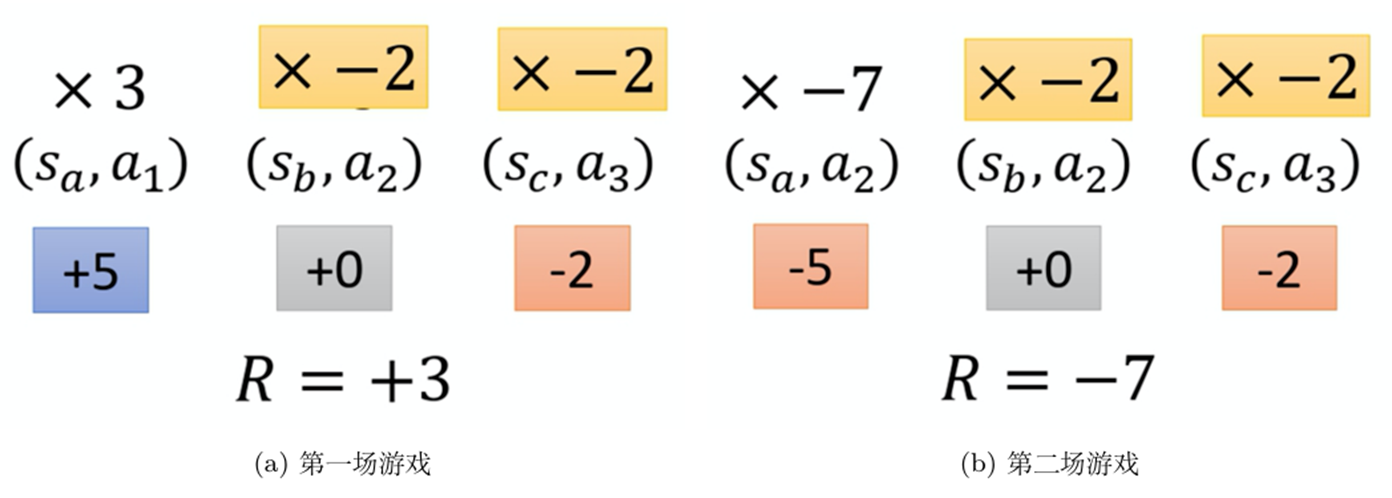
因此，一个合理的办法便是给每个状态-动作对分配合理的分数。

直观来看，一个时刻的动作执行后，只会影响后续的奖励，而与前面时刻的奖励无关。因此，可以将梯度改写为：

$\nabla\bar{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} G_t^n\nabla \log p_\theta(a_t^n|s_t^n)$

这样可以达到降低方差的作用，原因主要体现在如下两方面：

1. 相比于之前用整个轨迹的回报来更新轨迹中出现的状态-动作对，其减少了无关的前期奖励的影响，让每个状态动作对沿着正确的方向优化，降低了方差。
2. 相比于之前用整个轨迹的回报来更新轨迹中出现的状态-动作对，其对轨迹中的每步奖励 $r_t$ 的求和项变少了，因为 $r_t$ 其实是一个随机变量，减少了对随机变量的求和个数，降低每个随机变量叠加带来的偏差，从而降低方差。

通过这个技巧，便有了经典算法 REINFORCE，是由Williams与1992年提出的，其算法流程如下图：

3.2 添加基线

在前一个方法下，添加了一个基线，将梯度改写为：

$\begin{aligned} \nabla\bar{R}_\theta &= \mathbb{E}_{\tau}\left[\sum_{t=1}^{T_n-1}\left(G_t-b(s_t)\right)\nabla p_\theta(a_t|s_t)\right]\\ &\approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n-1} (G_t^n-b(s_t))\nabla \log p_\theta(a_t^n|s_t^n) \end{aligned}$

$b(s_t)$一般设为累积奖励期望 $E[s_t ]=E[r_t+\gamma r_{t+1}+…+\gamma^{T-1-t} r_{T-1)}]$，其不能与动作有关，因为我们在这里优化动作被选择的概率，依赖于策略的参数 $\theta$，若这个基线与动作有关，必然会牵扯到 $\theta$ ，在更新了 $\theta$ 后，$b(s_t)$ 的值也会变化，且变得不可控。

添加基线的作用：

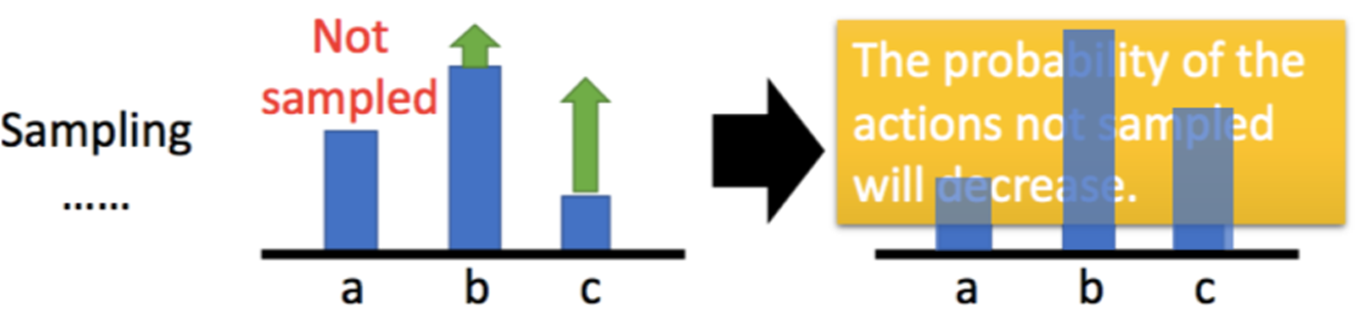
1. 让 $G_t^n-b(s_t)$ 成为有正有负的奖励，避免动作因未被采样到而降低出现概率，如下图，动作 a 未被采样，而另外两个动作被采样且获得了正回报，则这两个动作的概率会上升，而a的概率不变，因为最后所有的动作会经过一个 softmax 层，概率未改变的的动作 a 的概率会变成下降。因此需要平衡各个动作的价值，减掉一个基线，让其有正有负，如果我们得到的总奖励 $R(\tau) > b$，就让 $(s, a)$ 的概率上升。如果 $R(\tau) < b$，就算 $R(\tau)$ 是正的，值很小也是不好的，我们就让 $(s, a)$ 的概率下降，让这个状态采取这个动作的分数下降。
2. 相当于将 $G_t^n$ 中心化到均值附近，减小方差。
3. 减小方差加快学习速度（方差减小带来的）。

可以证明，在添加了基线之后，下述三个点是成立的：

1. 添加的基线的期望的梯度为 0
2. 原始优化目标的梯度的期望未发生改变
3. 方差减小

分别对应下面三个公式：

$\begin{aligned} \mathbb{E}_\tau\left[b(s_t)\nabla\log p_\theta(a_t|s_t)\right]&=0 \\ \mathbb{E}_\tau\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]&=\mathbb{E}_\tau\left[G_t\nabla\log p_\theta(a_t|s_t)\right]\\ Var_\tau\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]&<Var_\tau\left[G_t\nabla\log p_\theta(a_t|s_t)\right] \end{aligned}$

第一个点的证明如下：

$\begin{aligned} &\mathbb{E}_\tau[b(s_t)\nabla\log p_\theta(a_t|s_t)] \\ &=\sum_{s_t\in S}\mu(s_t)b(s_t)\sum_{a_t\in A}p_\theta(a_t|s_t)\nabla\log p_\theta(a_t|s_t)\\ &=\sum_{s_t\in S}\mu(s_t)b(s_t)\sum_{a_t\in A}p_\theta(a_t|s_t)\frac{\nabla p_\theta(a_t|s_t)}{p_\theta(a_t|s_t)}\\ &=\sum_{s_t\in S}\mu(s_t)b(s_t)\sum_{a_t\in A}\nabla p_\theta(a_t|s_t)\\ &=\sum_{s_t\in S}\mu(s_t)b(s_t)\nabla\sum_{a_t\in A}p_\theta(a_t|s_t)\\ &=\sum_{s_t\in S}\mu(s_t)b(s_t)\nabla (1)\\ &=0 \end{aligned}$

其中 $\mu(s_t)$ 是 $s_t$ 是在多条采样的轨迹中被采样的概率。

则第二个点显然成立，如下：

$\begin{aligned} &\mathbb{E}_\tau\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]\\ &=\mathbb{E}_\tau\left[G_t\nabla\log p_\theta(a_t|s_t)\right] - \mathbb{E}_\tau\left[b(s_t)\nabla\log p_\theta(a_t|s_t)\right]\\ &=\mathbb{E}_\tau\left[G_t\nabla\log p_\theta(a_t|s_t)\right] - 0\\ &=\mathbb{E}_\tau\left[G_t\nabla\log p_\theta(a_t|s_t)\right] \end{aligned}$

而第三个点则

$\begin{aligned} &Var_\tau\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]\\ &=\mathbb{E}_\tau[\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]^2]-[\mathbb{E}_\tau\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]]^2 \end{aligned}$

上式子中第二项未改变，而前一项如果小于原来的 $\mathbb{E}_\tau\left[[G_t\nabla\log p_\theta(a_t|s_t)\right]^2]$，那么就说明在添加了基线之后，其方差减小了。一个直观的理解就是当 $b(s_t)$ 为 $G_t$ 的期望的时候，$G_t-b(s_t)$ 都在零的附近，那么 $\left[(G_t-b(s_t))\nabla\log p_\theta(a_t|s_t)\right]$ 这一项就是 $\ge0$ 的，其比较接近于0，相比于原来的很大的一个数的平方，有明显的减少，所以方差是在减小的。详细的数学证明过程见链接，此处不深入展开。

综上，我们结合两种减少方差的方法，可以得到改进的REINFORCE算法，如下图所示。其中的 $b(s_t)$ 我们使用参数为 $w$ 的状态价值评估网络 $v(s)$ 进行代替，在一个轨迹采样完后，也需要同时对其进行更新，使其更准确的评估状态的价值。

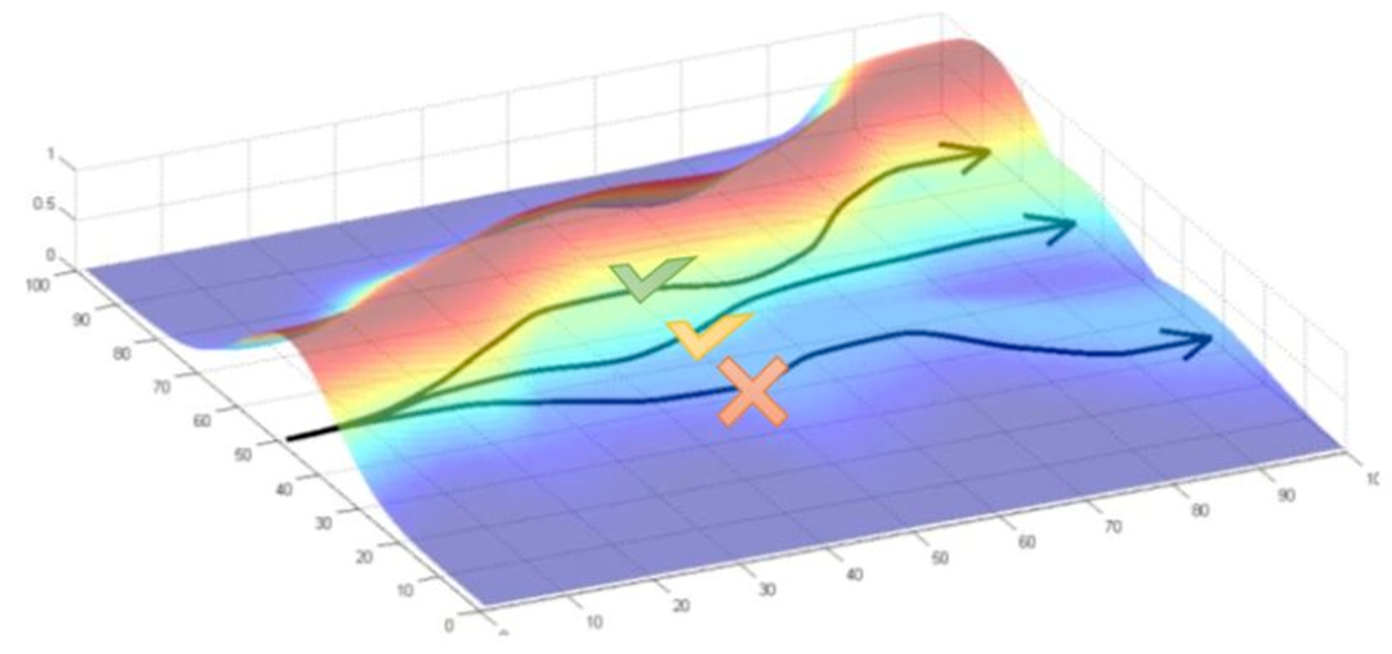
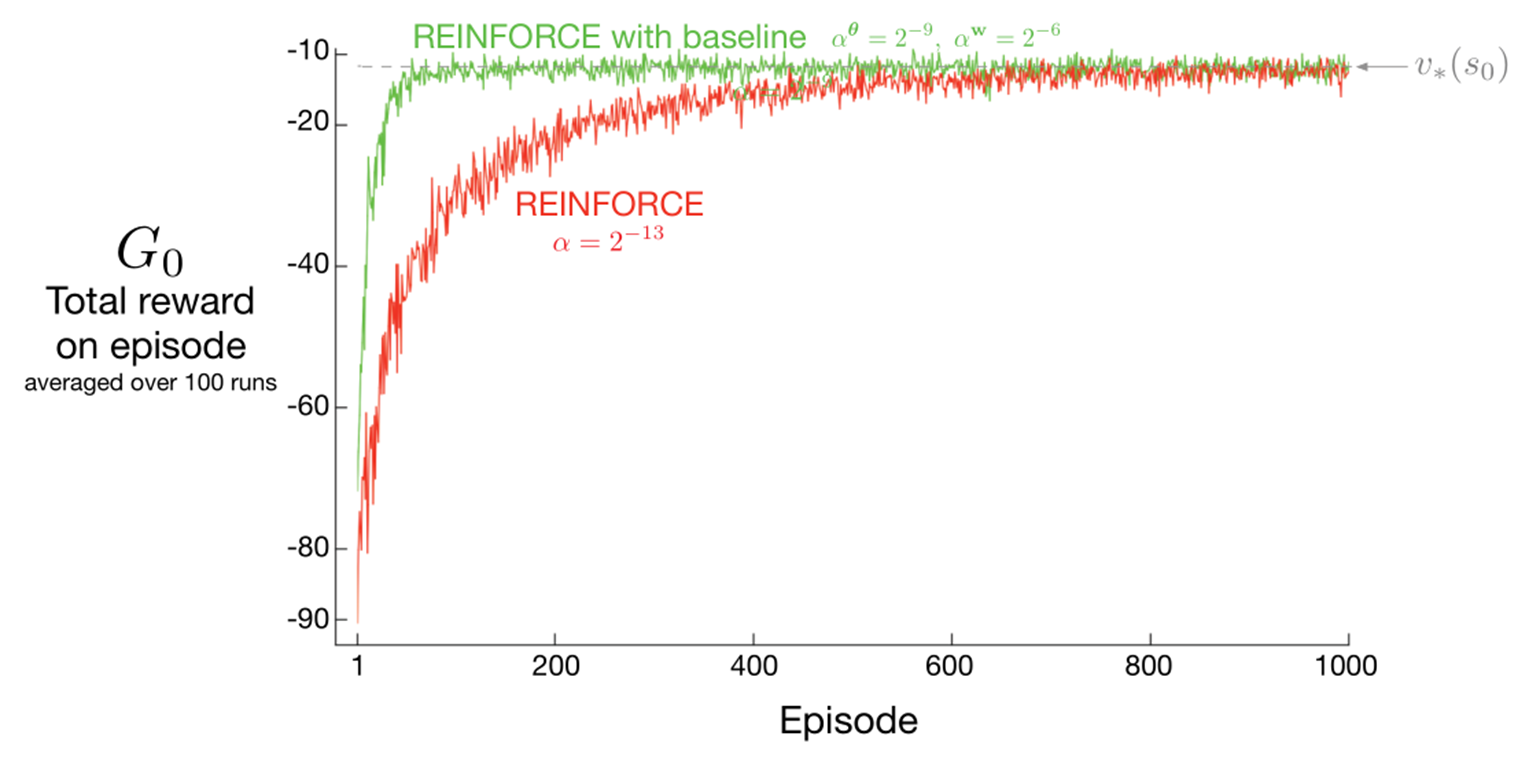
在使用了带基线的方法后，策略网络的学习速率明显加快，收敛的更快了，未带基线的REINFORCE在600回合以后才收敛，而带基线的在90回合便已经收敛，具体效果如下图（源自Sutton强化学习第二版）。

3.3 使用时序差分的方法

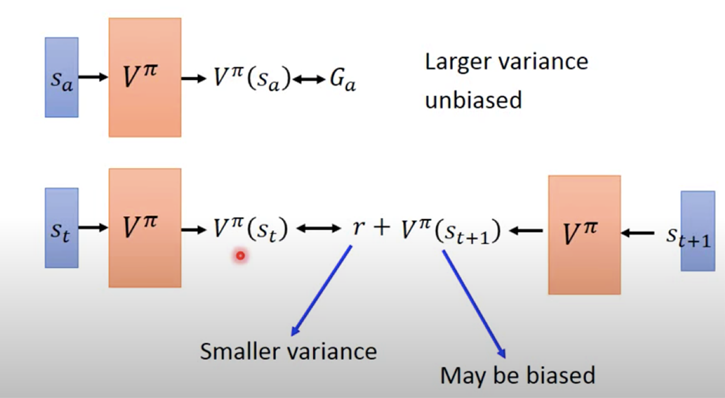
前文也提到，PG算法中大量的随机变量(指奖励$r_t$)进行求和，而每个随机变量的方差累加使得求和后的方差增大，那我们考虑单步更新，消除整个轨迹更新带来的大方差。这个方法就是时序差分方法(TD)，TD只用了一个时刻的即时奖励 $r$，所以相比MC而言可以避免方差累积的问题。

而TD算法具有代表性的便是演员-评论员(Actor-Critic, AC)算法，其包含策略网络和价值网络，是Policy-based和Value-based方法的结合。

尽管在3.2节的最后，我们使用状态价值函数 $v(s)$ 来评估状态的好坏，但它不是一种Actor-Critic算法，因为它的状态价值函数仅仅被用作基线，而不是一“个评论员”，即指其没有被用于自举操作（用后续时刻各个状态的价值估计值来更新当前状态的价值估计值），而只是作为被更新的状态价值的基线。

利用演员-评论员在较小步骤之内进行更新，能够减小方差，且能处理持续性问题（一个回合无穷无尽，不会终止），同时也可以在线学习。

这一部分会在后续的AC算法章节进行讲解，在此就不再继续深入了。

4 Policy-based的优缺点

4.1 优点

1. 直接对策略进行优化：策略梯度方法通过直接优化策略来寻找最优策略，不需要建立值函数模型，因此可以处理复杂的高维、连续状态空间问题，并且不受值函数估计的误差影响。
2. 支持非确定性策略：策略梯度方法可以处理非确定性策略，可以应对任务中存在噪声或随机性的情况，例如机器人控制中的摆臂控制问题。
3. 收敛速度较快：相比于值函数方法，策略梯度方法通常收敛速度更快，因为策略梯度方法可以直接通过策略空间中的梯度信息来更新策略参数，而值函数方法则需要通过值函数的迭代来逐步更新策略，而且要求轨迹探索得更全面，值函数的评估才准确，其策略更新才能更好。
4. 可以处理离散和连续动作空间：策略梯度方法可以处理离散和连续动作空间，可以应对不同类型的任务。

4.2 缺点

1. 容易陷入局部最优。
2. 由于策略梯度下降PG是需要不停的进行新数据的获取的，新的数据只会在当前的episode被使用，所以我们称之为on-policy策略。这样的策略会有一个明显的问题，一次神经网络的更新所采用的数据来自一局游戏，这显然不符合样本数据i.i.d(独立同分布)的要求。这个缺点会导致，对于简单游戏比如cart-pole和frozen-lake，原生PG或者优化的PG是可以比DQN等网络更快收敛，但面对更加复杂的环境时，便显得力不从心，经常出现无法收敛的情况。

5 参考文献

1. Sutton R S, Barto A G. Reinforcement learning: An introduction[M]. MIT press, 2018.
2. 王琦，杨毅远，江季，Easy RL：强化学习教程，人民邮电出版社，https://github.com/datawhalechina/easy-rl, 2022.