机器学习笔记(八)——决策树

1. 简介

决策树是一种基本的分类与回归算法。分类决策树模型是表示基于特征对实例进行分类的树形结构。决策树可以转换成一个if-then规则的集合，也可以看作是定义在特征空间划分上的类的条件概率分布。

2. 决策树模型

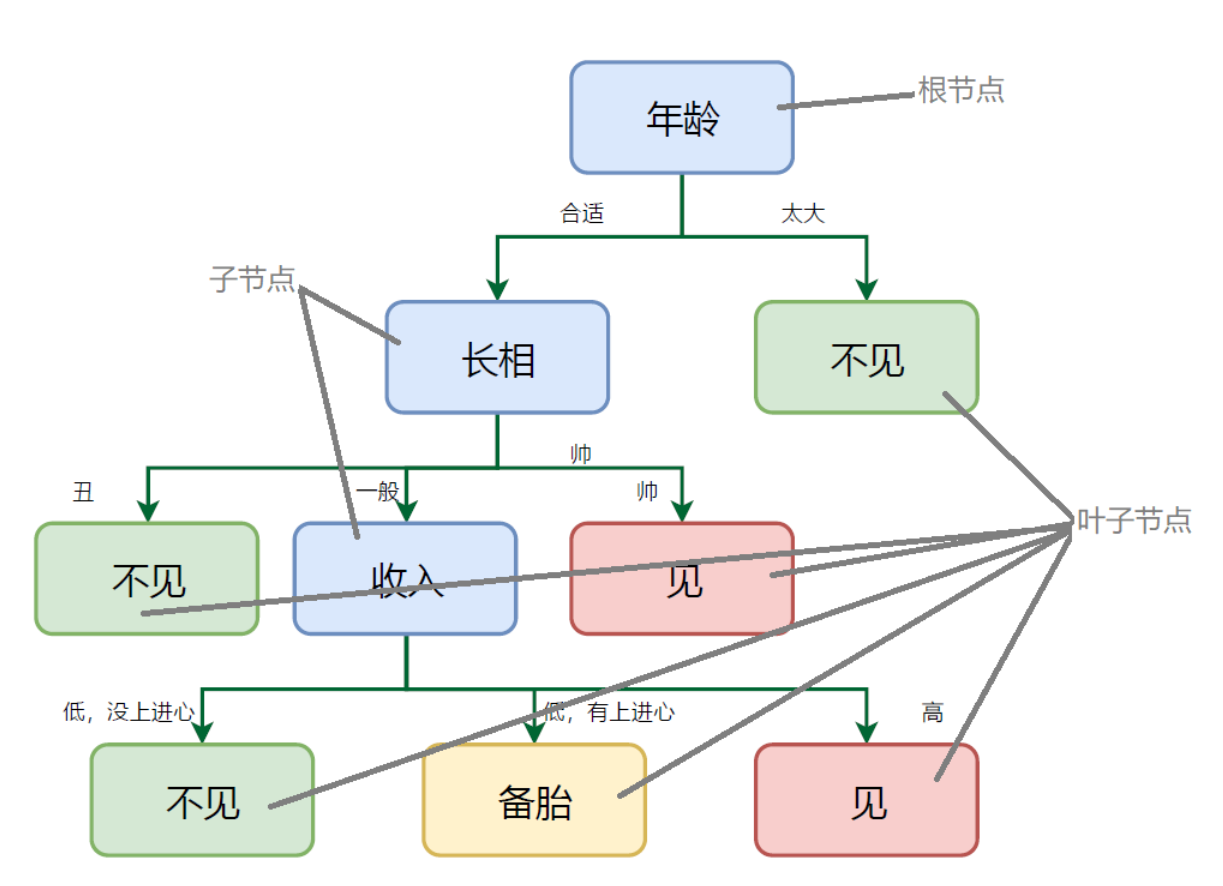
如上图所示，决策树是一种描述对实例进行分类的树形结构。决策树点由节点和有向边组成。节点有两种类型：内部节点和叶子节点。内部节点表示一个特征或属性，叶子节点表示一个类别。

决策树学习算法包括 3 部分：特征选择、树的生成和树的剪枝。常用的算法有 ID3、 C4.5 和 CART。

假设给定数据集

$D=\{(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)\}$

其中，$x_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(n)})^T$ 为输入实例（特征向量），$n$ 为特征个数， $y_i\in\{1,2,\cdots,K\}$ 为类别标记，$i = 1,2,\cdots,N$，$N$ 为样本容量。决策树模型的学习目标是根据给定的训练数据集构建一个决策树模型，使它能对实例进行正确的分类。

3. 特征选择

特征选择是决定用哪个特征来划分特征空间。

决策树的每个子节点（除开叶子节点）都代表对一种特征的划分，由该特征的不同属性值可以划分出对应的不同的子节点。但在每个非叶子节点中，选择那一个特征作为当前结点的划分依据呢？直观上来说，如果一个特征具有更好的分类能力，或者说，按照这一特征将训练数据划分为两个若干个子集，能使得各个子集在当前条件下有最好的分类，那么就应该选择这个特征。

通常使用信息增益、信息增益比和基尼指数作为特征选择的准则。

信息熵

信息论中的熵：是信息的度量单位，是一种对属性“不确定性的度量”。属性的不确定性越大，把它搞清楚所需要的信息量也就越大，熵也就越大。如果一个数据集 $D$ 有 $K$ 个类别（即为决策的种类数量），$p_i$ 代表该类别 $i $ 占全部样本的比例，则该数据集的熵为：

$H(D) = -\sum_{i=1}^{K}p_i\log_2p_i$

举例

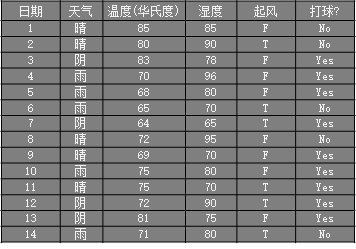
则对上图打球的数据集的熵为：

$Ent(14) = -(9/14)log_{2}(9/14)-(5/14)log_2(5/14)=0.940$

信息增益

样本集合对特征的信息增益（ID3）

$\begin{aligned} &g(D,A) = H(D)-H(D|A) \\ &H(D) = -\sum_{k=1}^{K}\frac{|C_k|}{|D|}\log_2\frac{|C_k|}{|D|} \\ &H(D|A) = \sum_{i=1}^{n}\frac{|D_i|}{|D|}H(D_i) \end{aligned}$

其中，$H(D)$ 是数据集 $D$ 的熵，$H(D_i)$ 是数据集 $D_i$ 的熵，$H(D|A)$ 是数据集 $D$ 对特征 $A$ 的条件熵。$D_i$ 是 $D$ 中特征 $A$ 取第 $i$ 个值的样本子集，$C_k$ 是 $D$ 中属于第 $k$ 类的样本子集。$n$ 是特征 $A$ 取值的个数，$K$ 是类的个数。

举例

则对上图打球数据集，计算天气属性的信息增益过程：

• 晴：打球记录 2 条，不打球记录 3 条

$Ent(D^1)=-(2/5)log_2(2/5)-(3/5)log_2(3/5)=0.97$

• 阴：打球记录 4 条，不打球记录 0 条

$Ent(D^2)=-(4/4)log_2(4/4)-(0/4)log_2(0/4)=0$

• 雨：打球记录 3 条， 不打球记录 2 条

$Ent(D^3)=-(3/5)log_2(3/5)-(2/5)log_2(2/5)=0.97$

其信息增益为：

$\begin{aligned} Gain(D,a)&=Ent(D)-\sum_{v=1}^{V}\frac{D^v}{D}Ent(D^v) \\&=0.94-\frac{5}{14}\times0.97-\frac{4}{14}\times0-\frac{5}{14}\times0.97\\&=0.247\end{aligned}$

同理，起风属性的信息增益为：0.048

再依次算出剩余两个属性的信息增益，选择最大的作为决策树的根结点。

信息增益比

样本集合对特征的信息增益比（C4.5）

$g_R(D,A)=\frac{g(D,A)}{H(D)}$

其中，$g(D,A)$ 是信息增益，$H(D)$ 是数据集 $D$ 的熵。

基尼指数

样本集合的基尼指数（CART）

$Gini(D) = 1-\sum_{k=1}^K\left(\frac{|C_k|}{|D|}\right)^2$

特征 $A$ 条件下集合 $D$ 的基尼指数：

$Gini(D,A) = \frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2)$

算法对比

4. 决策树生成

通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则。决策树的生成往往通过计算信息增益或其他指标，从根结点开始，递归地产生决策树。这相当于用信息增益或其他准则不断地选取局部最优的特征，或将训练集分割为能够基本正确分类的子集。

1. 初始化特征集合和数据集合；
2. 计算数据集合信息熵和所有特征的条件熵，选择信息增益最大（或信息增益最大）的特征作为当前决策节点；
3. 更新数据集合和特征集合（删除上一步使用的特征，并按照特征值来划分不同分支的数据集合）；
4. 若数据子集值包含单一特征，或数据子集只有一种类别，则为分支叶子节点，结束递归；否则，对分割出的数据子集递归重复执行 2，3 两步。

5. 决策树剪枝

预剪枝

在节点划分前来确定是否继续增长，及早停止增长的主要方法有：

• 节点内数据样本低于某一阈值；
• 所有节点特征都已分裂；
• 节点划分前准确率比划分后准确率高。

预剪枝不仅可以降低过拟合的风险而且还可以减少训练时间，但另一方面它是基于“贪心”策略，会带来欠拟合风险。

后剪枝

在已经生成的决策树上进行剪枝，从而得到简化版的剪枝决策树。

C4.5 采用的悲观剪枝方法，用递归的方式从低往上针对每一个非叶子节点，评估用一个最佳叶子节点去代替这课子树是否有益。如果剪枝后与剪枝前相比其错误率是保持或者下降，则这棵子树就可以被替换掉。C4.5 通过训练数据集上的错误分类数量来估算未知样本上的错误率。

后剪枝决策树的欠拟合风险很小，泛化性能往往优于预剪枝决策树。但同时其训练时间会大的多。

6. 案列

泰坦尼克号幸存者预测

• 数据格式

• 代码

import pandas as pd
from sklearn.tree import DecisionTreeClassifier, export_graphviz
from sklearn.metrics import classification_report
import pydotplus
from IPython.display import Image

# import os
# os.environ["PATH"] += os.pathsep + r'D:\Program Files\Graphviz\bin'

# 1 导入数据
data = pd.read_csv("./data/titanic_data.csv")
# print(data.head())

# 2 数据预处理
# 2.1 删除id列，对决策树的构建不起作用
data.drop(labels="PassengerId", axis=1, inplace=True)
# print(data.head())

# 2.2 将性别字段的字符串离散化，（sklearn处理不了离散的值）
data.loc[data["Sex"] == "male", "Sex"] = 1
data.loc[data["Sex"] == "female", "Sex"] = 0
# print(data.head())

# 2.3 补全年龄的缺失值，用平均值补充
data.fillna(value=data["Age"].mean(), inplace=True)
# print(data.head(10))

# 3 模型构建
Dtc = DecisionTreeClassifier(max_depth=5, random_state=8)
Dtc.fit(data.iloc[:, 1:], data["Survived"])

# 4 模型预测
pre = Dtc.predict(data.iloc[:, 1:])
report = classification_report(data["Survived"], pre)
print(report)

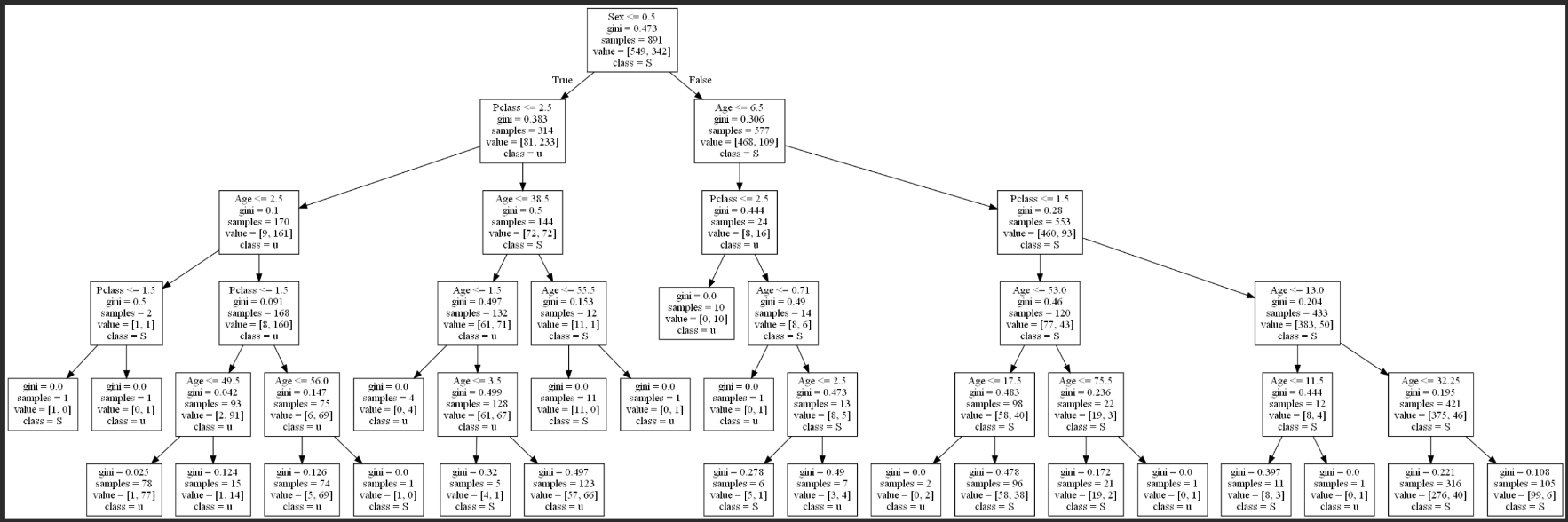
# 5 绘制决策树
dot_data = export_graphviz(Dtc, feature_names=["Pclass", "Sex", "Age"], class_names="Survived")
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write("tree.pdf")
Image(graph.create_png())
graph

• 结果

              precision    recall  f1-score   support

           0       0.84      0.88      0.86       549
           1       0.79      0.73      0.76       342

    accuracy                           0.82       891
   macro avg       0.82      0.81      0.81       891
weighted avg       0.82      0.82      0.82       891

引用

1. 李航——《统计学习方法》