张量分解

一、张量基本术语

1.1 阶(Order)

张量的阶，即为张量的维度大小。

1.2 纤维(Fibers)

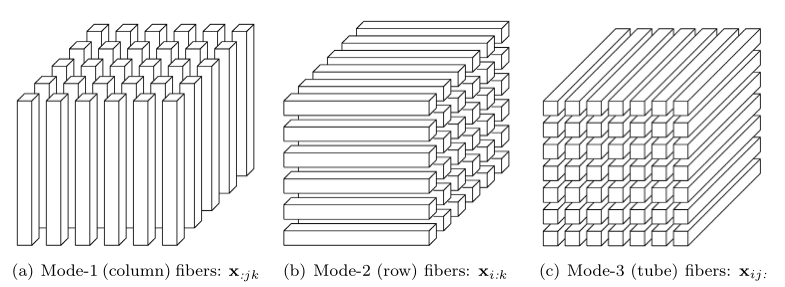
从张量中抽取出的一维向量，指固定其它维度，而某个维度的元素全部选取。

例： 有一个三阶张量 $X_{i,j,k}$ ，其列纤维（column fibers），行纤维（row fibers）和管纤维（tube fibers）如下图所示。

1.3 切片(Slice)

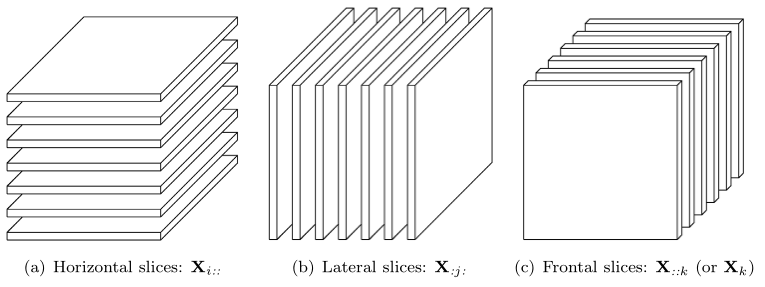
是张量的二维截面，除了两个维度，其他维度全部固定。

例： 有一个三阶张量 $X_{i,j,k}$ ，其水平切片（horizontal slices），横向切片（lateral slices）和前切片（frontal slices）如下图所示。

1.4 范数(Norm)

一个张量 $\mathcal{X}\in \mathbb{R}^{I_1\times I_2\times \cdots \times I_N}$ 的范数是所有元素的平方和开平方，记为 $||\mathcal{X}||$。

$||\mathcal{X}||=\sqrt{\sum_{i_1=1}^{I_1}\sum_{i_2=1}^{I_2}\cdots\sum_{i_N=1}^{I_N}x^2_{i_1i_2\cdots i_N}}$

1.5 内积(Inner product)

对于两个相同维度的张量 $\mathcal{X}, \mathcal{Y} \in \mathbb{R}^{I_1\times I_2\times\cdots\times I_N}$，他们的 内积 表示为对应（相同下标）元素的乘积的和，如下式子：

$\left \langle \mathcal{X},\mathcal{Y} \right \rangle = \sum_{i_1=1}^{I_1}\sum_{i_2=1}^{I_2}\cdots\sum_{i_N=1}^{I_N}x_{i_1i_2\cdots i_N}y_{i_1i_2\cdots i_N}$

可以发现，$\left \langle \mathcal{X},\mathcal{X} \right \rangle = ||\mathcal{X}||^2$ 。

1.6 Rank-one tensors

一种特殊的张量，如果一个 N 阶张量能表示为 N 个一维向量的外积(outer product)，那么该张量即为Rank-One Tensor，如下式子：

$\mathcal{X} = a^{(1)} \circ a^{(2)} \circ \cdots \circ a^{(N)}$

其中“$\circ$”符号代表外积操作。可以发现张量的每个元素为对应向量元素的乘积，即下式子成立：

$x_{i_1i_2\cdots i_N}=a_{i_1}^{(1)}a_{i_2}^{(2)}\cdots a_{i_N}^{(N)}$

1.7 对称性(Symmetry)

当一个张量的所有维度的大小都相同，可以称其为 立方体(cubical)。而当一个立方体的张量的每个元素在其下标的排列中仍保持不变，即可称该张量为 超对称的(supersymmetry) 。

例如，一个三阶张量 $\mathcal{X} \in \mathbb{R}^{I\times I \times I}$ 是超对称的当下式成立时满足：

$x_{ijk} = x_{ikj} = x_{jik} = x_{jki} = x_{kij} = x_{kji} \qquad i, j, k = 1, 2, \cdots, I$

更一般的情况，还存在局部对称，即在某两维或更多维是对称的情况。例如，三阶张量的前切面(frontal slices)是对称的二维矩阵。

1.8 对角张量(Diagonal tensors)

一个张量 $\mathcal{X}\in \mathbb{R}^{I_1\times I_2\times \cdots \times I_N}$ 是对角张量，当且仅当 $i_1 = i_2 = \cdots =i_N$ 时 $x_{i_1i_2\cdots i_N} \neq 0$ 。

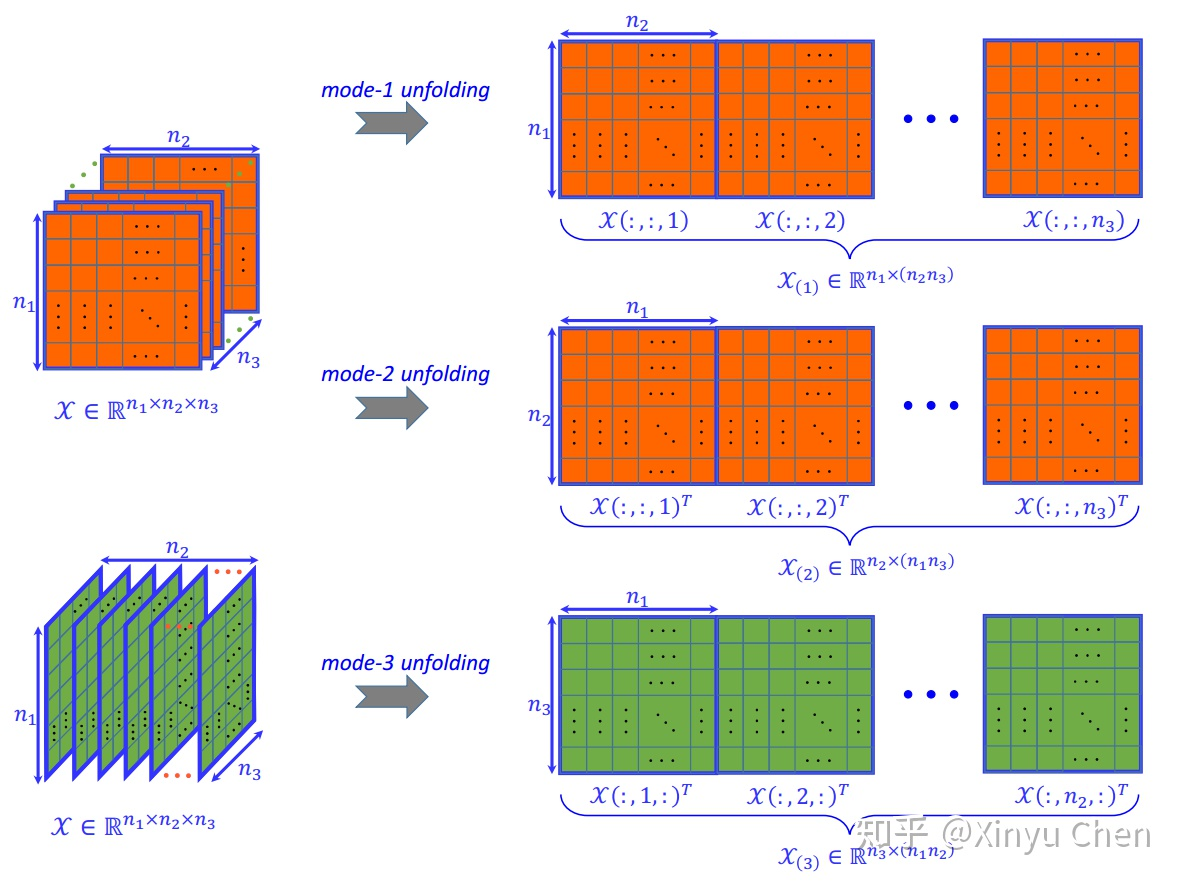
1.9 矩阵化(Matricization)

将高阶张量转化为一个矩阵，在此仅讨论mode-n 矩阵化。

对于三阶张量，有三种展开方式，如下图

1.10 张量乘法(Tensor multiplication)

张量乘矩阵

一个高阶张量 $\mathcal{X}\in\mathbb{R}^{I_1\times I_2\cdots\times I_N}$ 和一个二阶矩阵 $\mathbf{U} \in \mathbb{R}^ {J\times I_n}$ 的 n-mode 乘法如下：

$(\mathcal{X}\times_{n}\mathbf{U})_{i_1\cdots i_{n-1}ji_{n+1}\cdots i_N}=\sum_{i_n=1}^{I_n}x_{i_1i_2\cdots i_N}u_{ji_n}$

其他公式：

$\mathcal{Y} = \mathcal{X} \times_n \mathbf{U} \iff \mathbf{Y}_{(n)} = \mathbf{U}\mathbf{X}_{(n)}$

$\mathcal{X}\times_m \mathbf{A} \times_n \mathbf{B} = \mathcal{X}\times_n \mathbf{B} \times_m \mathbf{A} \quad (m \neq n)$

$\mathcal{X}\times_n \mathbf{A} \times_n \mathbf{B} = \mathcal{X}\times_n (\mathbf{BA})$

张量乘向量

一个高阶张量 $\mathcal{X}\in\mathbb{R}^{I_1\times I_2\cdots\times I_N}$ 和一个一维向量 $V \in \mathbb{R}^ {I_n}$ 的 n-mode 乘法如下：

$(\mathcal{X}\bar{\times}_{n}\mathbf{v})_{i_1\cdots i_{n-1}i_{n+1}\cdots i_N}=\sum_{i_n=1}^{I_n}x_{i_1i_2\cdots i_N}v_{i_n}$

其他公式：

$\mathcal{X} \ \bar\times_m \ \mathbf{a} \ \bar\times_n \ \mathbf{b} = (\mathcal{X} \ \bar\times_m \ \mathbf{a}) \ \bar\times_{n - 1} \ \mathbf{b} = (\mathcal{X} \ \bar\times_n \ \mathbf{b}) \ \bar\times_m \ \mathbf{a} \quad \text{for}\quad m < n$

上式中间部分，由于 $\mathcal{X}$ 与 $\mathbf{b}$ 相乘后维度减少一维，在 $m < n$ 的情况下，原来的第 $m$ 维消失，后面维度整体前移一维，所以原来的第 $n$ 维变为了 $n-1$ 维。

1.11 三种矩阵乘法

(1) Kronecker product

对于两个矩阵 $\mathbf{A} \in \mathbb{R}^{I \times J}$ ，$\mathbf{B} \in \mathbb{R}^{K \times L}$ ，其 Kronecker product 表示为 $\mathbf{A} \otimes \mathbf{B}$ ，其结果为 $(IK)\times(JL)$ 大小的矩阵：

$\begin{aligned} \mathbf{A} \otimes \mathbf{B} &= \begin{bmatrix} a_{11}\mathbf{B} & a_{12}\mathbf{B} & \cdots & a_{1J}\mathbf{B} \\ a_{21}\mathbf{B} & a_{22}\mathbf{B} & \cdots & a_{2J}\mathbf{B} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}\mathbf{B} & a_{I2}\mathbf{B} & \cdots & a_{IJ}\mathbf{B} \end{bmatrix} \\ &=\begin{bmatrix} \mathbf{a}_1\otimes\mathbf{b}_1 & \mathbf{a}_1\otimes\mathbf{b}_2 & \mathbf{a}_1\otimes\mathbf{b}_3 & \cdots & \mathbf{a}_J\otimes\mathbf{b}_{L-1} & \mathbf{a}_J\otimes\mathbf{b}_L\end{bmatrix} \end{aligned}$

如下例子：

$\begin{bmatrix}1 & 2 \\ 3 & 1 \end{bmatrix} \otimes \begin{bmatrix}0 & 3 \\ 2 & 1 \end{bmatrix}= \begin{bmatrix} 1\cdot 0 & 1 \cdot 3 & 2\cdot 0 & 2\cdot 3 \\ 1\cdot 2 & 1 \cdot 1 & 2\cdot 2 & 2\cdot 1 \\ 3\cdot 0 & 3 \cdot 3 & 1\cdot 0 & 1\cdot 3 \\ 3\cdot 2 & 3 \cdot 1 & 1\cdot 2 & 1\cdot 1 \end{bmatrix}= \begin{bmatrix} 0 & 3 & 0 & 6 \\ 2 & 1 & 4 & 2 \\ 0 & 9 & 0 & 3 \\ 6 & 3 & 2 & 1 \end{bmatrix}$

(2) Khatri-Rao product

对于两个矩阵 $\mathbf{A} \in \mathbb{R}^{I \times K}$ ，$\mathbf{B} \in \mathbb{R}^{J \times K}$ ，其 Khatri-Rao product 表示为 $\mathbf{A} \odot \mathbf{B}$ ，其结果为 $(IJ)\times K$ 大小的矩阵：

$\mathbf{A}\odot \mathbf{B}=\begin{bmatrix}\mathbf{a}_1\otimes \mathbf{b}_1 & \mathbf{a}_2\otimes \mathbf{b}_2 & \cdots & \mathbf{a}_K\otimes \mathbf{b}_K \end{bmatrix}$

它由两个矩阵对应的列向量的Kronecker积排列而成。因此，Khatri-Rao积又叫做对应列Kronecker积。

注： 若 $a$，$b$ 是向量，则有 $a\otimes b=a\odot b$ 。

(3) Hadamard product

按张量的对应元素相乘，需要两个矩阵的大小相同。对于两个矩阵 $\mathbf{A} \in \mathbb{R}^{I\times J}$ ，$\mathbf{B} \in \mathbb{R}^{I\times J}$ ，其 Hadamard product 表示为 $\mathbf{A} * \mathbf{B}$ ，其结果为 $I\times J$ 大小的矩阵：

$\mathbf{A}*\mathbf{B}= \begin{bmatrix} a_{11}b_{11} & a_{12}b_{12} & \cdots & a_{1J}b_{1J} \\ a_{21}b_{21} & a_{22}b_{22} & \cdots & a_{2J}b_{2J} \\ \vdots & \vdots & \ddots & \vdots \\ a_{I1}b_{I1} & a_{I2}b_{I2} & \cdots & a_{IJ}b_{IJ} \end{bmatrix}$

二、张量的Tucker分解

Tucker分解是SVD分解的高阶形式，其将张量分解为一个核张量与每一维度上对应矩阵的乘积。具体来说，以三阶张量 $\mathcal{X} \in \mathbb{R}^{I \times J \times K}$ 为例，其Tucker分解写为如下形式：

$\begin{aligned} \mathcal{X} &\approx \mathcal{G} \times_1 \mathbf{A} \times_2 \mathbf{B} \times_3 \mathbf{C} \\ & = \sum_{p=1}^{P} \sum_{q=1}^{Q} \sum_{r=1}^{R} g_{pqr} \ \mathbf{a}_p \circ\mathbf{b}_q \circ \mathbf{c}_r \\ &= [[\mathcal{G};\mathbf{A}, \mathbf{B}, \mathbf{C}]] \end{aligned}$

其中，$\mathbf{A} \in \mathbb{R}^{I \times P}$，$\mathbf{B} \in \mathbb{R}^{J \times Q}$，$\mathbf{C} \in \mathbb{R}^{K \times R}$ 是不同维度上的因子矩阵，这些矩阵通常被认为是不同维度上的主成分。$\mathcal{G}\in\mathbb{R}^{P\times Q\times R}$ 称为核张量，其中的每个元素代表了不同成分之间的交互程度。

从元素的角度看，Tucker分解可以写为：

$\mathbf{X}_{ijk} \approx \sum_{p=1}^{P} \sum_{q=1}^{Q} \sum_{r=1}^{R} \mathbf{g}_{pqr} \mathbf{a}_{ip} \mathbf{b}_{jq} \mathbf{c}_{kr} \\ i = 1,\cdots,I,\quad j=1,\cdots,J,\quad k=1,\cdots,K$

$\mathbf{P}$，$\mathbf{Q}$和$\mathbf{R}$是因子矩阵 $\mathbf{A,B,C}$ 的成分数(例如因子矩阵的列数)。如果 $\mathbf{P}$，$\mathbf{Q}$和$\mathbf{R}$ 小于$\mathbf{I,J,K}$，那么张量 $\mathcal{G}$ 可以被认为是张量 $\mathcal{X}$ 的压缩版本。

2.1 HOSVD算法

2.2 HOOI算法

若 $\mathcal{X}$ 是一个大小为 $I_1\times I_2 \times \cdots \times I_N$ 的 N 阶张量，那么计算 Tucker 分解要解决的优化问题为

$min \left \Vert \mathcal{X} - [[\mathcal{G}; \mathbf{A}^{(1)}, \mathbf{A}^{(2)},\cdots,\mathbf{A}^{(N)}]] \right \Vert \tag{1}$

其中，$\mathcal{G} \in \mathbb{R}^{R_1 \times R_2 \times \cdots \times R_N}$， 矩阵 $\mathbf{A}^{(n)} \in \mathbb{R} ^{I_n \times R_n}$ 且列正交。

如果在最优解处，那么核张量 $\mathcal{G}$ 必然满足

$\mathcal{G} = \mathcal{X} \times_1 (\mathbf{A}^{(1)})^T \times_2 (\mathbf{A}^{(2)})^T \times_3 \cdots \times_N (\mathbf{A}^{(N)})^T \tag{2}$

将上式导入到公式(1)中，那么优化目标可以重写为：

$\begin{aligned} &\left \Vert \mathcal{X}- [[\mathcal{G};\mathbf{A}^{(1)}, \mathbf{A}^{(2)},\cdots,\mathbf{A}^{(N)}]] \right \Vert^2 \\ &\qquad = \left \Vert \mathcal{X} \right \Vert^2 - 2 \left \langle \mathcal{X}, [[\mathcal{G};\mathbf{A}^{(1)}, \mathbf{A}^{(2)},\cdots,\mathbf{A}^{(N)}]] \right \rangle + \left \Vert [[\mathcal{G};\mathbf{A}^{(1)}, \mathbf{A}^{(2)},\cdots,\mathbf{A}^{(N)}]] \right \Vert^2 \\ &\qquad = \left \Vert \mathcal{X} \right \Vert^2 - 2 \left \langle \mathcal{X}\times_1 (\mathbf{A}^{(1)})^T\times_2\cdots \times_N(\mathbf{A}^{(N)})^T, \mathcal{G} \right \rangle + ||\mathcal{G}||^2 \\ &\qquad = \left \Vert \mathcal{X} \right \Vert^2 - 2 \left \langle \mathcal{G}, \mathcal{G} \right \rangle + \left \Vert \mathcal{G} \right \Vert^2 \\ &\qquad = \left \Vert \mathcal{X} \right \Vert^2 - \left \Vert \mathcal{G} \right \Vert^2 \\ &\qquad = \left \Vert \mathcal{X} \right \Vert^2 - \left \Vert \mathcal{X}\times_1 (\mathbf{A}^{(1)})^T\times_2\cdots \times_N(\mathbf{A}^{(N)})^T \right \Vert^2 \end{aligned}$

最小化上述式子，即最大化下式：

$\max_{\mathbf{A}^{(n)}} \left \Vert \mathcal{X}\times_1 (\mathbf{A}^{(1)})^T\times_2\cdots \times_N(\mathbf{A}^{(N)})^T \right \Vert \\ \text{subject to} \quad \mathbf{A^{(n)}} \in \mathbb{R}^{I_n \times R_n} \quad \text{and columnwise orthogonal}$