机器学习笔记(七)——BP神经网络

一、BP 网络结构定义

1.1 本文所用的神经网络

本文推导所使用的是三层神经网络，包含输入层、隐层和输出层，每层网络都有多个神经元，激活函数为 $sigmoid$函数， 具体形式如下图。

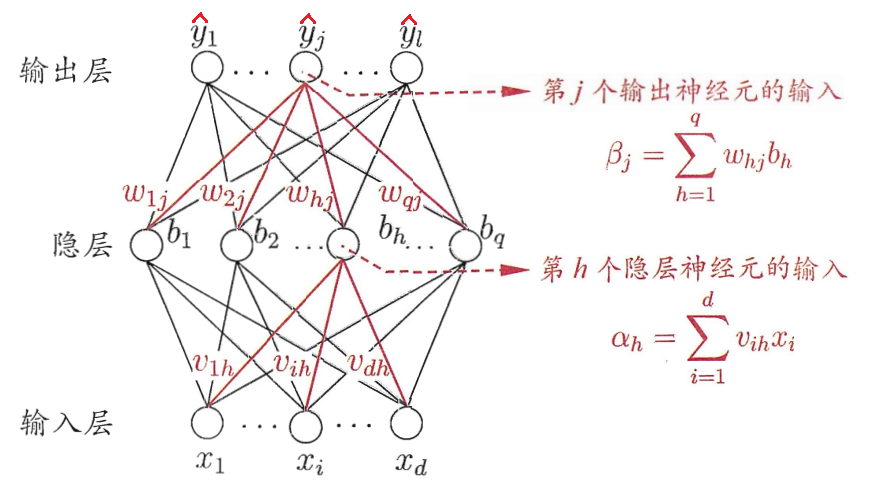
1.2 符号说明

$d$ 代表输入层的神经元个数，$q$ 代表隐层神经元的个数，$l$ 代表输出层神经元的个数；

$x_i$ 代表输入层的第 $i$ 个神经元；

$v_{i,h}$ 代表输入层第 $i$ 个神经元映射到隐层第 $h$ 个神经元的连接权值；

$\gamma_h$ 代表映射到隐层第 $h$ 个神经元的输入层神经元的线性组合的偏置项，也等价于 $v_{0,h}$；

$\alpha_h$的说明如上图；

$b_h=g(\alpha_h + \gamma_h)=(\sum\limits_{i=1}^{d}v_{i,h}x_i + \gamma_h)$，其中函数 $g$ 为 $sigmoid$ 函数，$b_h$ 即为隐层第 $h$ 个神经元的输出；

$w_{h,j}$ 代表隐层第 $h$ 个神经元映射到输出层第 $j$ 个神经元的连接权值；

$\theta_h$ 代表映射到输出层第 $j$ 神经元的隐层神经元的线性组合的偏置项，也等价于 $w_{0,j}$ ；

$\beta_j$的说明如上图；

$\hat y_j=g(\beta_j + \theta_j)=(\sum\limits_{h=1}^{q}w_{h,j}b_h + \theta_j)$，其中函数 $g$ 为 $sigmoid$ 函数，$\hat y_j$ 即为输出层第 $j$ 个神经元的输出，即为整个模型的预测值；

$y_j$ 代表样本实际的标签，真实值；

$Y^k$ 代表第 $k$ 个训练样本的真实标签，$Y_j^k$ 代表第 $k$ 个训练样本的标签的第 $j$ 个元素，$\hat Y^k$ 代表第 $k$ 个训练样本的预测结果，$\hat Y_j^k$ 代表第 $k$ 个训练样本的预测结果中的第 $j$ 个元素。

二、BP神经网络推导

2.1 前项传播

由本文神经网络的图片定义可以知道其前项传播的路径如下（从上到下对应网络的输入层到输出层）：

$\begin{aligned} &x_i \\ &\alpha= \sum_{i=1}^{d}v_{i,h}x_i\\ &b_h = g(\alpha_h+\gamma_h)\\ &\beta_j = \sum_{h=1}^{q}w_{h,j}b_h\\ &\hat y_j = g(\beta_j + \theta_j) \end{aligned}$

2.2 代价函数

单个样本

由前一小结，其在第 $k$ 个训练样本上的代价函数(均方误差)为：

$J_k = \frac{1}{2}\sum_{j=1}^{l}(\hat y_j - y_j)$

下面是Logistic回归的代价函数形式（极大似然估计）：

$J_k = -\sum_{j=1}^{l}[y_j log(\hat y_j) + (1-y_j)log(1-\hat y_j)]$

全样本

而其在全样本上的代价函数为：

$J = \frac{1}{2m}\sum_{k=1}^{m}\sum_{j=1}^{l}(\hat Y_j^k - Y_j^k)$

同上，下面也是Logistic回归的全样本代价函数形式：

$J = -\frac{1}{m}\sum_{k=1}^{m}\sum_{j=1}^{l}[Y_j^k log(\hat Y_j^k) + (1-Y_j^k)log(1-\hat Y_j^k)]$

2.3 反向传播求各层权值的梯度

则接下来可以由链式法则反向对 $J$ 求偏导得出网络中各层之间的连接权值。为简化计算，使用平方误差函数计算单样本上的梯度，计算如下：

1. 隐层到输出层之间的连接权值：

$\begin{aligned} \nabla_{w_{h,j}} &= \frac{\partial J}{\partial w_{h,j}}\\ &= \frac{\partial J}{\partial \hat y_j} \frac{\partial \hat y_j}{\partial \beta_j} \frac{\partial \beta_j}{\partial w_{h,j}}\\ &= (\hat y_j - y_j) \cdot \hat y_j(1-\hat y_j) \cdot b_h\\ &= \hat y_j(1 - \hat y_j)(\hat y_j - y_j)b_h \end{aligned}$

2. 隐层到输出层之间的偏置：

$\begin{aligned} \nabla_{\theta_j} &= \frac{\partial J}{\partial \theta_j} \iff \nabla_{w_{0,j}}\\ &= \frac{\partial J}{\partial \hat y_j} \frac{\partial \hat y_j}{\partial \theta_j}\\ &= (\hat y_j - y_j) \cdot \hat y_j(1-\hat y_j)\\ &= \hat y_j(1 - \hat y_j)(\hat y_j - y_j) \end{aligned}$

3. 输入层到隐层的连接权值：

$\begin{aligned} \nabla_{v_{i,h}} &= \frac{\partial J}{\partial v_{i,h}}\\ &= \sum_{j=1}^{l} \frac{\partial J}{\partial \hat y_j} \frac{\partial \hat y_j}{\partial \beta_j} \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \alpha_h} \frac{\partial \alpha_h}{\partial v_{i,h}}\\ &= \sum_{j=1}^{l} (\hat y_j - y_j) \cdot \hat y_j(1-\hat y_j) \cdot w_{h,j} \cdot b_h(1-b_h) \cdot x_i\\ &= x_i b_h(1-b_h) \sum_{j=1}^{l} \hat y_j(1 - \hat y_j)(\hat y_j - y_j)w_{h,j} \end{aligned}$

4. 输入层到输出层的偏置：

$\begin{aligned} \nabla_{\gamma_h} &= \frac{\partial J}{\partial \gamma_h} \iff \nabla_{v_{0,h}}\\ &= \sum_{j=1}^{l} \frac{\partial J}{\partial \hat y_j} \frac{\partial \hat y_j}{\partial \beta_j} \frac{\partial \beta_j}{\partial b_h} \frac{\partial b_h}{\partial \gamma_h}\\ &= \sum_{j=1}^{l} (\hat y_j - y_j) \cdot \hat y_j(1-\hat y_j) \cdot w_{h,j} \cdot b_h(1-b_h)\\ &= b_h(1-b_h) \sum_{j=1}^{l} \hat y_j(1 - \hat y_j)(\hat y_j - y_j)w_{h,j} \end{aligned}$

上述仅仅是对单个训练样本中的梯度，因此我们需要把所有样本上的对应参数的梯度累加起来，得到最终该的权值梯度。

三、手写数字分类识别实战

数据集包含 5000 张 $20\times 20$ 像素的数字图片，每张图片的数字为 $[0, 9]$ 之间，在数据集中，每一张图片按照像素矩阵的列优先存储展开为一个一维的大小为 400 的数组。

这里使用了两种方案进行分类识别：

1. 一种是给每个数字训练一个Logstic回归分类器，若是该数字，分类结果为大于0.5，若不是该数字，分类结果小于0.5，训练好10个模型后，给每个预测样本，经过十个模型的预测后，比较哪个数字对应的分类器最接近1，即该数字即为样本的数字类别。
2. 另一种是构建三层人工神经网络进行分类，输入层神经元为400个，代表输入样本的特征个数，隐层神经元为25个（可不一致），将神经网络的输出层神经元设为10个，代表样本在每个数字类别上的概率，其最大概率的数字即为类别。

实验结果发现在第一种方案每个模型迭代 500 次后能达到 96.5% 的分类识别准确率，而第二种在迭代 100 次后就能达到 99.3% 的分类识别准确率。

两种方案的代码链接如下：

1. 多个 Logistic 回归分类器的实现方式：ex3.ipynb
2. BP 神经网络的实现方式：ex4_nn.ipynb