机器学习笔记(五)——k 近邻法

本文部分内容引用于 李航《统计学习方法》 一书

1. 模型阐述

kNN（k 近邻算法，k-nearest neighbor）是一种基本的 分类 与 回归 方法。PS：本文中仅讨论其在 分类 问题中的使用。

kNN 的输入为实例的特征向量，输出为实例对应的类别（可以为多类别）。

kNN 的原理是：对于新的分类样本实例，根据其最近邻的 k 个训练实例的类别，通过多数表决或其它更有效的方法决定该样本实例的类别。

kNN 不具有显示的学习过程。

kNN 模型的三个基本要素为 k 值的选择、距离度量 和 分类决策规则。

当确定了模型的 训练集、距离度量、k 值 以及 分类决策规则 后，对于任何一个新的样本实例的输入，其所属的类别唯一确定。

1.1 模型给出

给定一个数据集：

$T = \{(x_1, y_1),(x_2, y_2),\cdots, (x_m, y_m)\}$

其 kNN 的分类模型为（决策规则为 多数表决 的情况）：

$f(x') = arg\max_{c_j}\sum_{x_i\in N_k(x')}I(y_i=c_j)$

其参数说明如下：

1. $m$ 和 $n$ 代表 样本数量 和 特征种类数量 ；
2. $x_i \in R^n$，代表第 $i$ 个样本的 特征空间，$x_{i,j}$ 代表第 $i$ 个样本的第 $j$ 个特征，其中 $i=1,2,\cdots,m.\ j=1,2,\cdots,n$；
3. $y_i\in\{c_1,c_2,\cdots c_K\}$ 代表第 $i$ 个样本的类别；
4. $x'\in R^n$ 代表一个 新的样本实例；
5. $N_k(x')$ 代表距离新样本实例 $x'$ 最近的 $k$ 个训练样本的集合；
6. $I$ 为指示函数，当参数为 true 时，结果为 1，否则为 0。

1.2 距离度量

特征空间中两个实例点的距离是两个实例点相似程度的反映。在 kNN 模型中的特征空间一般为 $n$ 维向量空间 $R^n$，使用的距离为 欧氏距离 或 闵可夫斯基距离（$L_p$ 距离）。

$L_p$ 距离的定义如下：

$L_p(x_i, x_j) = (\sum_{k=1}^n|x_{i,k}-x_{j,k}|)^{\frac{1}{p}}$

式中 $p\ge1$，$x_{i,k}$ 代表第 $i$ 个样本的第 $k$ 个特征，$x_{j,k}$ 代表第 $j$ 个样本的第 $k$ 个特征。

当 $p=1$ 时，称为 曼哈顿距离，为

$L_1(x_i,x_j)=\sum_{k=1}^n|x_{i,k}-x_{j,k}|$

当 $p=2$ 时，称为 欧氏距离，为

$L_2(x_i,x_j)=(\sum_{k=1}^n|x_{i,k}-x_{j,k}|^2)^{\frac{1}{2}}$

当 $p=+\infty$ 时，它为各个坐标距离的最大值，即为：

$L_\infty(x_i,x_j)=\max_{k}|x_{i,k}-x_{j,k}|$

注：使用不同的距离度量所确定的最近邻点是不同的。

1.3 k 值选择

k 值的选择将会对 k 近邻法的结果产生较大影响。

如果 k 值选择的比较小，相当于用较小的领域中的训练实例进行预测，学习的近似误差会减小，但估计误差会增大。k 值减小意味着整体模型变得复杂，容易发生过拟合。

如果 k 值选择的比较大，相当于用较大的领域中的训练实例进行预测，可以减少学习的估计误差，但学习的近似误差会增大。k 值增大意味着模型变得简单。

如果 $k = n$，那么无论输入实例为什么，都将简单的预测为在所有训练样本中出现最多的类别。

在应用中， k 值一般取较小值，通常采用 交叉验证法 选取最优的 k 值。

1.4 分类决策规则

kNN 模型中的分类决策规则往往是多数表决，即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。

2 案例实现

2.1 样本数据描述

此处我们仍然使用 sklearn 库内置的经典数据集—— 鸢尾花 数据集。

观察数据集发现其前一百个样本包含 0 和 1 两个类别，且为了方便可视化展示，我们仅选取其中的两个特征，花萼长度 和 花萼宽度，将其分类绘制二维平面散点图如下：

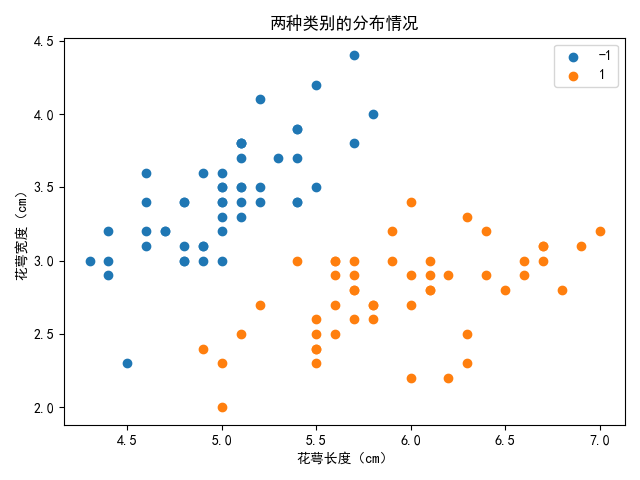
2.2 代码实现

因KDtree不便于实现，这里使用的算法为线性扫描训练样本求距离。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris


class Model:
    """
    knn模型，线性扫描求近邻
    """

    def __init__(self, x, y, k=1, p=2) -> None:
        """
        初始化模型参数
        @param x: 模型训练样本 x
        @param y: 模型训练标签 y
        @param k: 近邻节点数量
        @param p: 距离度量中的L_p距离，p=1为曼哈顿距离，p=2为欧氏距离，p=np.inf为各个坐标下的距离最大值
        """
        self.m, self.n = x.shape[0], x.shape[1]
        self.x, self.y = x, y
        self.k, self.p = k, p

    def predict_one(self, x):
        """
        预测一个点的类别
        """
        knn_list = []  # 存放当前最近邻的 k 个训练样本点的 距离和类别
        for i in range(self.k):
            # 正则化，对应求 x与self.x 的L_p距离
            d = np.linalg.norm(x - self.x[i], ord=self.p)
            knn_list.append((d, self.y[i]))

        for i in range(self.k, self.m):
            # 找到knn_list中当前最远距离的样本的下标
            max_index = knn_list.index(max(knn_list, key=lambda t: t[0]))
            # 计算第 i 个训练样本与测试样本的l_p距离
            d = np.linalg.norm(x - self.x[i], ord=self.p)
            if knn_list[max_index][0] > d:  # 若第 i 个训练样本的距离小于当前k近邻中的最远距离点，则替换掉最远点
                knn_list[max_index] = (d, self.y[i])

        knn = [p[1] for p in knn_list]  # k个近邻的训练样本对应的类别列表
        mp = {knn[0]: 1}  # 统计各种类别出现次数的字典
        max_count_class = knn[0]  # k近邻中出现次数最多的样本类别
        for i in range(1, len(knn)):
            if mp.get(knn[i], 0) == 0:
                mp[knn[i]] = 1
            else:
                mp[knn[i]] += 1
            if mp[knn[i]] > mp[max_count_class]:
                max_count_class = knn[i]

        return max_count_class

    def predict(self, X):
        """
        预测一系列点的类别
        """
        return np.array([self.predict_one(x) for x in X])


# 导入数据集
data = load_iris()

# 数据提取
X = data["data"][:100, :2]  # 取前100样本的前两种特征
y = data["target"][:100]

test_X = np.array([[7.59268006, 3.72002957],
                   [4.62328497, 4.3367199],
                   [5.8765327,  4.11724536],
                   [5.5044102,  2.9900012],
                   [7.24050913, 4.04598368],
                   [7.8199658,  4.44725224],
                   [5.43502613, 2.02691898],
                   [5.16360786, 4.32145775],
                   [6.11587685, 2.6084383],
                   [7.26444409, 3.51119187]])
test_y = np.array([1, 0, 0, 1, 1,  1,  1, 0,  1,  1])

model = Model(X, y, k=3, p=2) # k值取3，距离为欧氏距离
pred = model.predict(test_X)
print("预测类别：", pred)

acc = np.sum(test_y == pred) / len(pred)
print("分类准确率：%.2f%%" % (acc * 100))


# 绘制散点图-观察数据分布情况
plt.figure()
plt.scatter(X[:50, 0], X[:50, 1], label="0")
plt.scatter(X[50:, 0], X[50:, 1], label="1")
plt.scatter(test_X[pred == 0, 0], test_X[pred == 0, 1],
            c='red', label='pred_0')
plt.scatter(test_X[pred == 1, 0], test_X[pred == 1, 1],
            c='black', label='pred_1')
plt.legend()
plt.xlabel("花萼长度（cm）")
plt.ylabel("花萼宽度（cm）")
plt.title("两种类别的分布情况")
plt.show()

2.3 输出结果

预测类别： [1 0 0 1 1 1 1 0 1 1]
分类准确率：100.00%

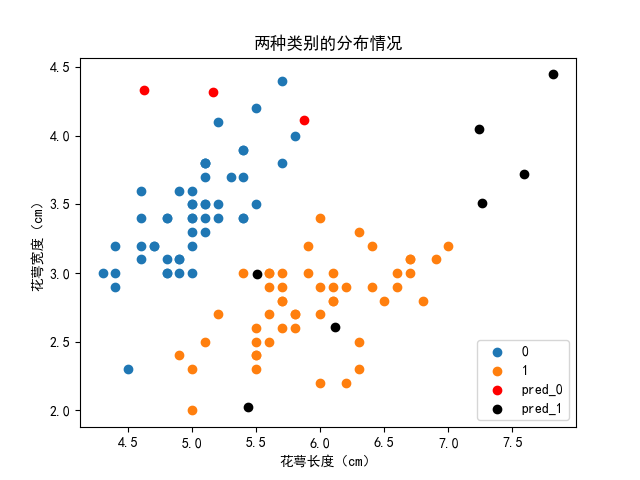
其分类结果在二维散点图如下图所示，其中红色点为预测为类别 0 的点，黑色点为预测为类别 1 的点。可以看到预测的结果还是挺不错的。