机器学习笔记(四)——感知机

本文部分内容引用于 李航《统计学习方法》 一书

1. 模型阐述

感知机（Perceptron）是二分类的线性分类模型，其输入为实例的特征向量，输出为实例的类别，取 $+1$ 和 $-1$ 值。

1.1 模型给出

给定一个数据集：

$T = \{(x_1, y_1),(x_2, y_2),\cdots, (x_m, y_m)\}$

其感知机的二分类模型为：

$f(x_i) = sign(w\cdot x_i+b)$

参数说明如下：

1. $m$ 和 $n$ 代表样本数量和特征种类数量；
2. $x_i \in R^n$，代表第 $i$ 个样本的特征空间，$x_{i,j}$ 代表第 $i$ 个样本的 第 $j$ 个特征，其中 $i=1,2,\cdots,m.\ j=1,2,\cdots,n$；
3. $y_i\in\{-1, +1\}$ 代表第 $i$ 个样本的类别，只有正例和反例两个类别；
4. $sign$ 为符号函数，即为：

$sign(x)= \begin{cases} +1, &x\ge 0\\ -1, &x<0 \end{cases}$

5. $w\in R^n$ 为感知机模型的参数，代表权值向量(weight vector)；
6. $b\in R$ 也为感知机模型的参数，代表偏置(bias)；
7. $w\cdot x_i$ 代表权值向量和某个样本特征空间的内积。

1.2 损失函数（Loss function）

这里的损失函数区别于代价函数：

• 损失函数：是基于单个样本的，是一个样本的误差；
• 代价函数：是定义在整个训练集上的，是全部样本的损失函数的均值。

定义感知机模型的损失函数如下：

$L(w,b)= -\sum_{x_i\in M} y_i(w\cdot x_i+b)$

其中， $M$ 为误分类的样本的集合。我们的目标便是找到最小化 $L(w,b)$ 的参数 $w$ 和 $b$。

另外，也有将损失函数定义为(参见 邱锡鹏 —《神经网络与深度学习》中的 3.4 节)：

$L(w,b)=\max_{x_i\in M}\{-y_iw\cdot x_i\}$

1.3 随机梯度下降(Stochastic gradient descent)

上述损失函数的梯度变化如下：

$\begin{aligned} \nabla_wL(w,b) &= -\sum_{x_i\in M}y_ix_i\\ \nabla_bL(w,b) &= -\sum_{x_i\in M}y_i \end{aligned}$

起初，随机选择超平面 $w_0, b_0$，使用梯度下降不断地极小化损失函数。在极小化过程中不是每次将所有的误分类点的梯度下降，而是随机取一个误分类的点使其梯度下降。每次仅选取一个误分类的样本点 $(x_i, y_i)$，对 $w,b$ 进行更新：

$\begin{aligned} w &\leftarrow w + \alpha y_ix_i\\ b &\leftarrow b + \alpha y_i \end{aligned}$

其中 $\alpha$ 为学习速率。重复上述单样本更新的过程，直到损失函数降为 0。

2. 案例实现

2.1 样本数据描述

此处我们使用 sklearn 库内置的经典数据集—— 鸢尾花 数据集。

观察数据集发现其前一百个样本包含 0 和 1 两个类别，且为了方便可视化展示，我们仅选取其中的两个特征，花萼长度 和 花萼宽度，将其分类绘制二维平面散点图如下：

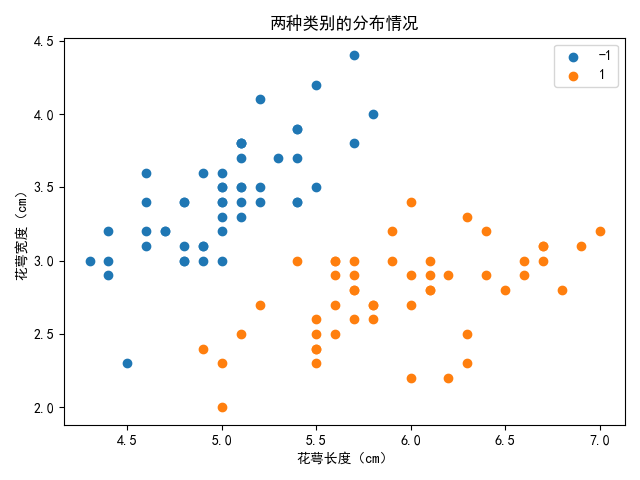
接下来，我们的任务就是按照感知机的实现思路，编写代码来找到分离超平面，将这两种类别的数据合理的划分开来。

2.2 代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris

# 导入数据集
data = load_iris()
# print(data["data"][:50])
# print(data["feature_names"])

# 数据提取
X = data["data"][:100, :2]  # 取前100样本的前两种特征
y = data["target"][:100]
# 将 y 中类别 0 变为类别 -1
y[y == 0] = -1

# 绘制散点图-观察数据分布情况
plt.figure()
plt.scatter(X[:50, 0], X[:50, 1], label="-1")
plt.scatter(X[50:, 0], X[50:, 1], label="1")
plt.legend()
plt.xlabel("花萼长度（cm）")
plt.ylabel("花萼宽度（cm）")
plt.title("两种类别的分布情况")
plt.show()


class Model:
    """
    线性二分类感知机模型
    """
    alpha = 0  # 学习率
    max_iter = 0  # 最大迭代次数
    x, y = None, None  # 样本特征和标签
    w = None  # 超平面权值向量 (weight vector)
    b = None  # 偏置项 (bias)
    loss_list = None

    def __init__(self, alpha=0.01, max_iter=10000):
        """
        初始化模型
        :param alpha: 学习率
        :param max_iter: 最大迭代次数
        """
        self.alpha = alpha
        self.max_iter = max_iter

    def __sign(self, x):
        """
        符号函数
        """
        ty = [1 if tx >= 0 else -1 for tx in x]
        return np.array(ty)

    def __Loss(self, x, y):
        """
        计算损失函数
        :param x: 错误分类样本特征
        :param y: 错误分类样本标签
        :return: 损失函数
        """
        if len(y) == 0:
            return 0
        return -np.inner(y, (np.dot(x, self.w) + self.b))

    def fit(self, x, y):
        """
        进行模型训练
        :param x: 训练样本的特征
        :param y: 训练样本的标签
        """
        self.loss_list = []
        x, y = x.astype(np.float64), y.astype(np.float64)
        self.x, self.y = x, y
        m, n = x.shape[0], x.shape[1]

        # 初始化参数，全 0
        self.w = np.zeros(n)
        self.b = 0

        # 迭代训练
        for k in range(self.max_iter):
            flag = False  # 是否存在误分类样本的标记
            false_x, false_y = None, None  # 存放误分类样本的列表
            for i in range(m):
                tx, ty = x[i], y[i]
                if ty * (np.inner(self.w, tx) + self.b) <= 0:
                    """误分类样本"""
                    flag = True
                    if false_x is None:
                        false_x = np.array([tx])
                        false_y = np.array([ty])
                    else:
                        false_x = np.concatenate((false_x, [tx]))
                        false_y = np.append(false_y, ty)

            if flag:  # 出现错误分类
                # 计算损失函数
                L = self.__Loss(false_x, false_y)
                self.loss_list.append(L)

                # 随机取一个误分类样本修改梯度
                k = np.random.randint(0, len(false_y))
                tx, ty = false_x[k], false_y[k]
                self.w += self.alpha * ty * tx
                self.b += self.alpha * ty
            else:  # 未出现分类错误的点，结束迭代
                self.loss_list.append(0)
                print("Well done!")
                return
        print("Not completed!")  # 在最大迭代次数下未找到最优

    def get_param(self):
        """
        获取训练好的模型参数
        :return: 权值向量,偏置
        """
        return self.w, self.b

    def plot_loss_change(self):
        """绘制损失函数的变化趋势"""
        plt.figure()
        plt.plot(self.get_loss_list(), linewidth=".4")
        plt.xlabel("iter")
        plt.ylabel("loss")
        plt.title("损失函数值随迭代次数增加的变化趋势")
        plt.show()

    def get_loss_list(self):
        """返回模型训练时的损失函数变化列表"""
        return np.array(self.loss_list)

    def predict(self, x):
        """
        用训练好的模型进行预测
        :param x:
        :return: 预测得到的类别
        """
        pred = np.dot(x, self.w) + self.b
        return self.__sign(pred)


model = Model(alpha=0.1, max_iter=10000)
model.fit(X, y)
w, b = model.get_param()

# 打印权值向量和偏置
print("weigth vector:")
print(w)
print("bias:")
print(b)

# 打印损失函数列表
# print(model.get_loss_list())

# 绘制损失函数变化趋势
model.plot_loss_change()

# 生成一系列横坐标在 [4, 8] 之间的点（和散点的横坐标范围大致相同），
#     用于绘制超平面，其中二维空间的 (x, y) 坐标对应特征 (x0, x1)
# tx = np.array([i for i in range(4, 8, 0.5)])
tx = np.arange(4, 8, 0.5)
# 由式子(超平面) w0 * x0 + w1 * x1 + b = 0 推出 x1 = -(w0 * x0 + b) / w1
ty = -(w[0] * tx + b) / w[1]

# 绘制超平面分割数据
plt.figure()
plt.plot(tx, ty, color="red", label="separating")
plt.scatter(X[:50, 0], X[:50, 1], label="-1")
plt.scatter(X[50:, 0], X[50:, 1], label="1")
plt.legend()
plt.xlabel("花萼长度(cm)")
plt.ylabel("花萼宽度(cm)")
plt.title("分离超平面划分结果")
plt.show()

2.3 结果输出

注：由于是随机选取误分类样本进行梯度计算去修正权值向量和偏置，每次运行代码得到的结果可能不同，存在误差，但其结果都是在最优解附近，均为可行解。

Well done!
weigth vector:
[ 6.33 -8.  ]
bias:
-10.09999999999998

上述结果，代表分离超平面为：

$6.33x_0 - 8x_1 - 10.1 = 0$

其划分结果如下图所示：

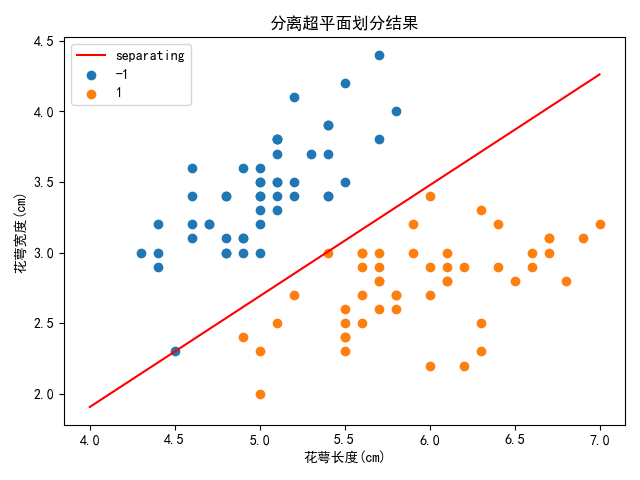
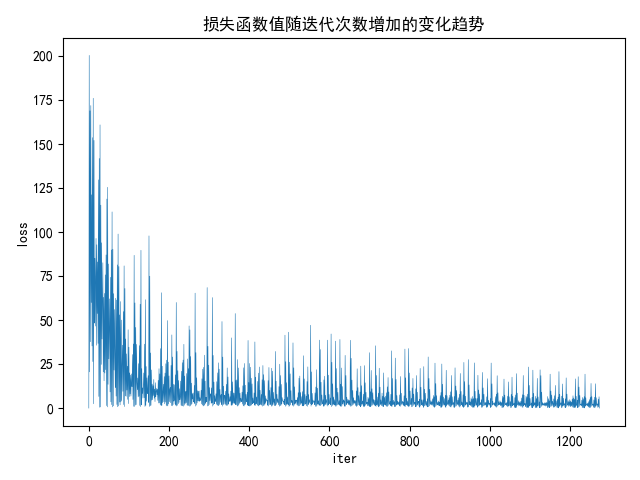
然后，绘制出训练过程中损失函数的变化曲线图如下：