机器学习笔记(二)——单变量的线性回归

1. 单变量线性回归模型表示

对于只有一维特征向量的回归问题：

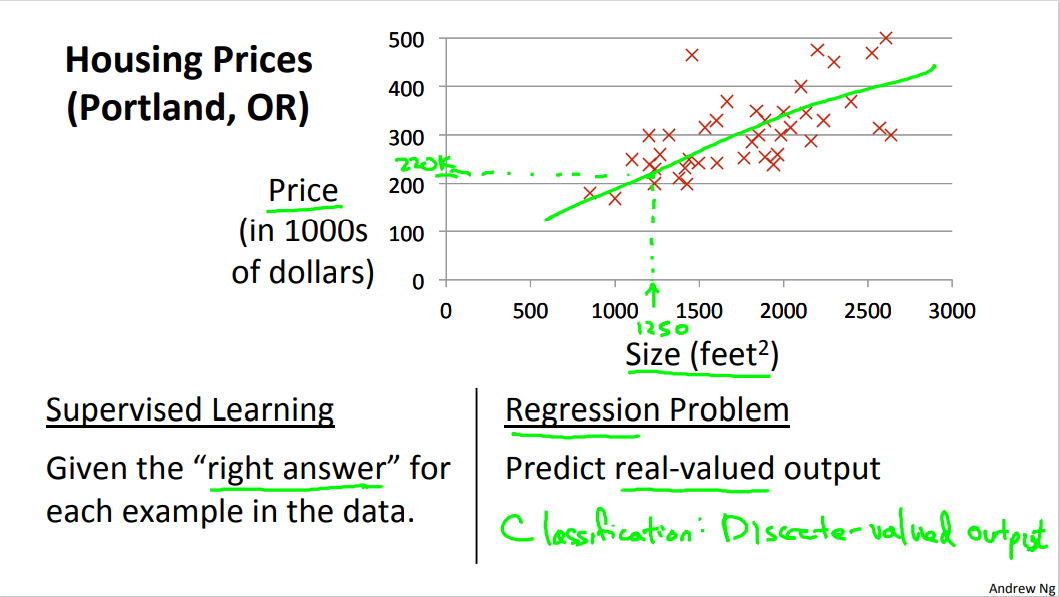
• $x$ 和 $y$ 为真实样本的特征和标签集合
• $x_i$ 和 $y_i$ 代表第 $i$ 个样本的特征和标签
• $m$ 代表样本数量
• $h_\theta$ 为假设函数(hypothesis function)
• $\theta_0$ 和 $\theta_1$ 分别为假设函数的两个参数

使用以下假设函数的式子来拟合出数据点，我们要找到合适的 $\theta_0$ 和 $\theta_1$，使 $h_\theta(x)$ 逼近 $y$:

$h_\theta(x)=\theta_0 + \theta_1x$

那么如何判别我们用假设函数 $h_\theta$ 拟合出来的曲线与原样本中数据点的逼近程度呢？这里使用的是计算 代价函数 的大小进行判断。

2. 代价函数(Cost function)

在上面的模型中，随着 $\theta_0$ 和 $\theta_1$ 这两个参数的值的不同，会产生不同的假设函数，即产生不同的直线。我们使用 平方误差函数 来计算 模型误差，用以衡量假设函数的好坏。

平方误差函数(Squared error function)

$J(\theta_0, \theta_1) = \frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i) - y_i)^2$

通过不断调整 $\theta_0$ 和 $\theta_1$ 的值，使得模型误差最小，即可以得到在使用线性函数进行拟合时的最好假设函数。即如下式子所示：

$arg\,\min_{\theta_0, \theta_1} J(\theta_0, \theta_1)$

可以发现，随着 $\theta_0$ 和 $\theta_1$ 的变化，拟合出来的直线与真实值 $y$ 的误差如下图：

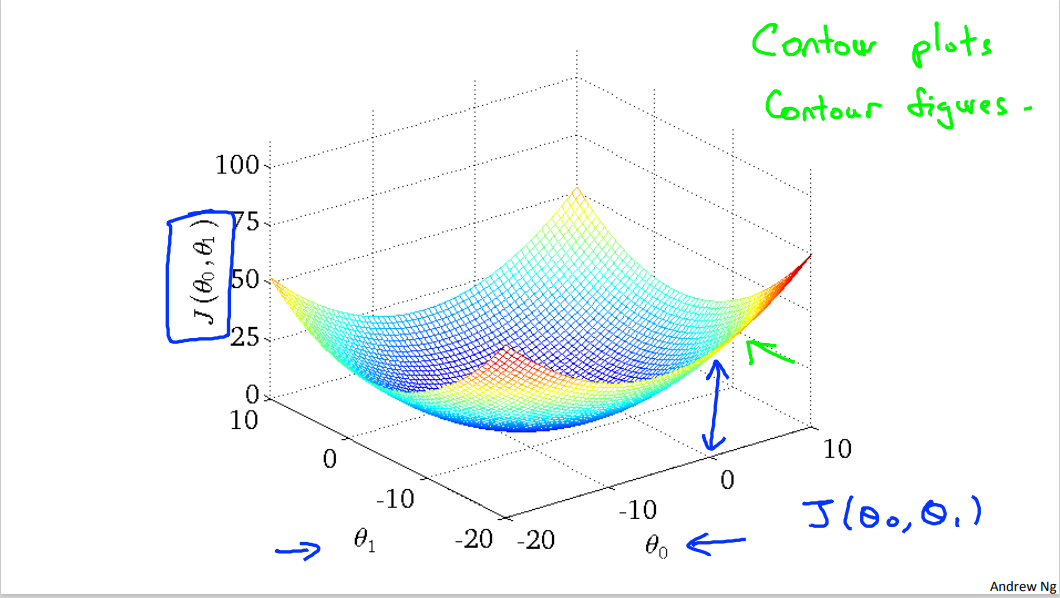
3. 梯度下降(Gradient descent)

在上一节，我们发现假设函数随着两个参数 $\theta_0$ 和 $\theta_1$ 的变化，其拟合出的直线与真实值的误差也在变化，但因为两个参数为连续的，如何避免大量的计算，而快速的找到最小误差对应的参数呢？

梯度下降 便是用来快速找到最优的代价函数的方法。其依据计算出在不同参数上的方向导数进行 同时更新 $\theta_0$ 和 $\theta_1$， 直到其不再变化则达到最优结果。

$\theta_0 = \theta_0 - \alpha\frac{\partial}{\partial \theta_0}J(\theta_0, \theta_1)\\ \theta_1 = \theta_1 - \alpha\frac{\partial}{\partial \theta_1}J(\theta_0, \theta_1)$

上式子中 $\alpha$ 代表 学习速率，其决定每次更新时向下走的距离有多大。

4. 案例实现

这里随机产生 20 个样本 $x$，并构造一个一阶线性函数 $f(x) = 1 + 2x$ 进行计算出 $y$。再构造 $h_\theta(x)$ 来逼近 $f(x)$，使用梯度下降来计算出假设函数 $h_\theta$ 的参数 $\theta_0$ 和 $\theta_1$。

代码实现

import numpy as np
import matplotlib.pyplot as plt


class MyLiner:
    """
    单变量线性函数的拟合类
    使用梯度下降法
    """
    theta0 = 0
    theta1 = 0
    __alpha = 0  # 下降速率
    __eps = 0  # 梯度变化小于此精度则认定不在变化
    __iters = 0  # 迭代次数

    __x = None  # 一维
    __y = None  # 一维

    def __h(self, x):
        """
        假设函数 h
        :param x: 传入特征
        :return: 特征 x 在此假设函数下的映射
        """
        return self.theta0 + self.theta1 * x

    def __J(self):
        """
        平均误差函数
        :return:
        """
        return np.sum((self.__h(self.__x) - self.__y) ** 2) / (2 * len(self.__x))

    def __gd(self):
        """
        梯度下降以及更新
        :return: 更新后的 theta0 和 theta1
        """
        t0 = np.mean(self.theta0 + self.theta1 * self.__x - self.__y)
        t1 = np.mean(self.theta1 * (self.__x ** 2) + self.theta0 * self.__x - self.__x * self.__y)
        return self.theta0 - self.__alpha * t0, self.theta1 - self.__alpha * t1

    def __init__(self, alpha=0.1, eps=1e-5, iters=10000):
        """
        构造函数
        :param alpha: 学习步长
        :param eps: 精度
        """
        self.__alpha = alpha
        self.__eps = eps
        self.__iters = iters

    def fit(self, x, y):
        """
        进行训练
        :param x: 特征向量
        :param y: 标签
        """
        self.__x, self.__y = x.astype(np.float64), y.astype(np.float64)

        # 随机找一个起点
        self.theta0 = np.random.randint(10)
        self.theta1 = np.random.randint(10)

        t_j = self.__J()
        for i in range(self.__iters):  # 进行迭代
            [self.theta0, self.theta1] = self.__gd()
            tj = self.__J()
        return tj

    def get_param(self):
        """
        获取拟合最优的参数
        :return: [theta_0, theta_1]
        """
        return [self.theta0, self.theta1]

    def predict(self, x):
        """
        预测
        :param x: 要预测的特征
        :return: 预测的结果
        """
        return self.__h(x)


def f(x, a=1, b=1):
    """自定义线性函数"""
    return a * x + b


# 生成 x 和 y
x = np.random.randint(20, size=(20))
# 让其在y轴上随机偏移[-1,1]
y = f(x, 2, 1) - np.random.random((20)) * 2 + 1

# 构建模型
model = MyLiner(alpha=0.01, iters=10000)
res = model.fit(x, y)
print(res)  # 输出平均误差 J(theta_0, theta_1)
print(model.get_param())  # 假设函数的参数 [theta_0, theta_1]
pred = model.predict(x)

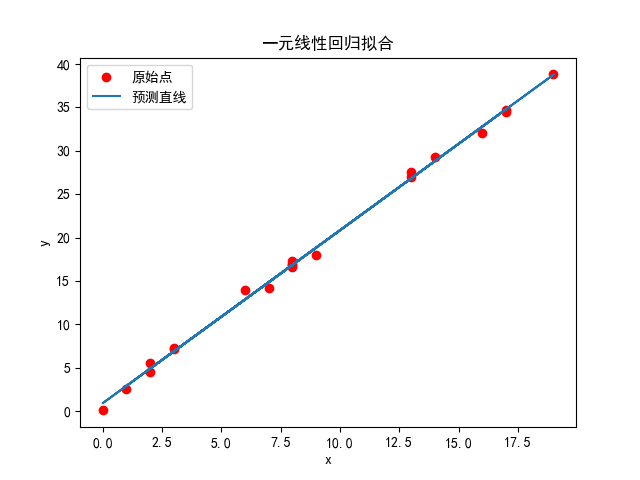
# 绘图
plt.figure()
plt.scatter(x, y, c="red", label="原始点")
plt.plot(x, pred, label="预测直线")
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.title("一元线性回归拟合")
plt.savefig("./fig1.png")
plt.show()

输出结果

0.13860587282095355
[0.8923516892592014, 1.9940981295109517]