2018年第九届蓝桥杯省赛-G.螺旋折线

2022-03-23 · 66次阅读 · 原创 · 数据结构与算法

#蓝桥杯 #题解 #数学

原题链接

题面

如下图所示的螺旋折线经过平面上所有整点恰好一次。

折线图

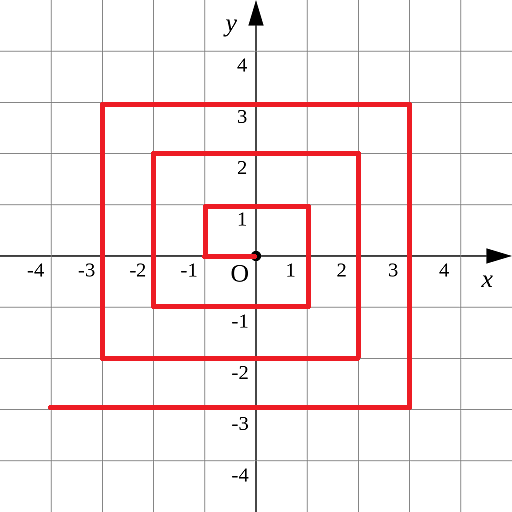
对于整点 (X, Y)，我们定义它到原点的距离 dis(X, Y) 是从原点到 (X, Y) 的螺旋折线段的长度。

例如 dis(0, 1)=3, dis(-2, -1)=9。

给出整点坐标 (X, Y)，你能计算出 dis(X, Y) 吗？

输入描述

输入格式：

输入一行，X 和 Y ， $-10^9 \leq X, Y \leq 10^9$ 。

输出描述

输出 dis(X, Y)。

输入样例

0 1

输出样例

题解

数学

首先，在图中找规律，可以发现：

在第一象限的拐点刚好在对角线上，而对于第一象限对角线上的点 $(k, k)$ ，从原点到这个点的距离为 $(2k) ^2$ 。观察还发现，x 轴上方的横线和 y 轴右侧的竖线都有对应的一个第一象限对角线上的点与其相连，则对于 x 周上方的横线上的点 $(xx, yy)$ ，其对应的对角线上的点为 $(yy, yy)$ ，对于 y 轴右侧的点 $(xx, yy)$ ，其对应的对角线上的点为 $(xx, xx)$ ，再减去获增加与对角线在水平获垂直方向的位移差，就可以得到答案。
在第三象限和 x 轴负半轴的顶拐点都落在 $y = x + 1$ 这条直线上，记拐点坐标为 $(k, k + 1)$ ，则原点到其的距离为 $(2\times(-k) - 1) ^ 2 = (2k + 1)^2$ 。同理，y 轴左侧的竖线和 x 轴下方的横线都与 $y = x + 1$ 这条直线有交点，则可以利用两条直线上的点与拐点上的位移差计算出来结果。

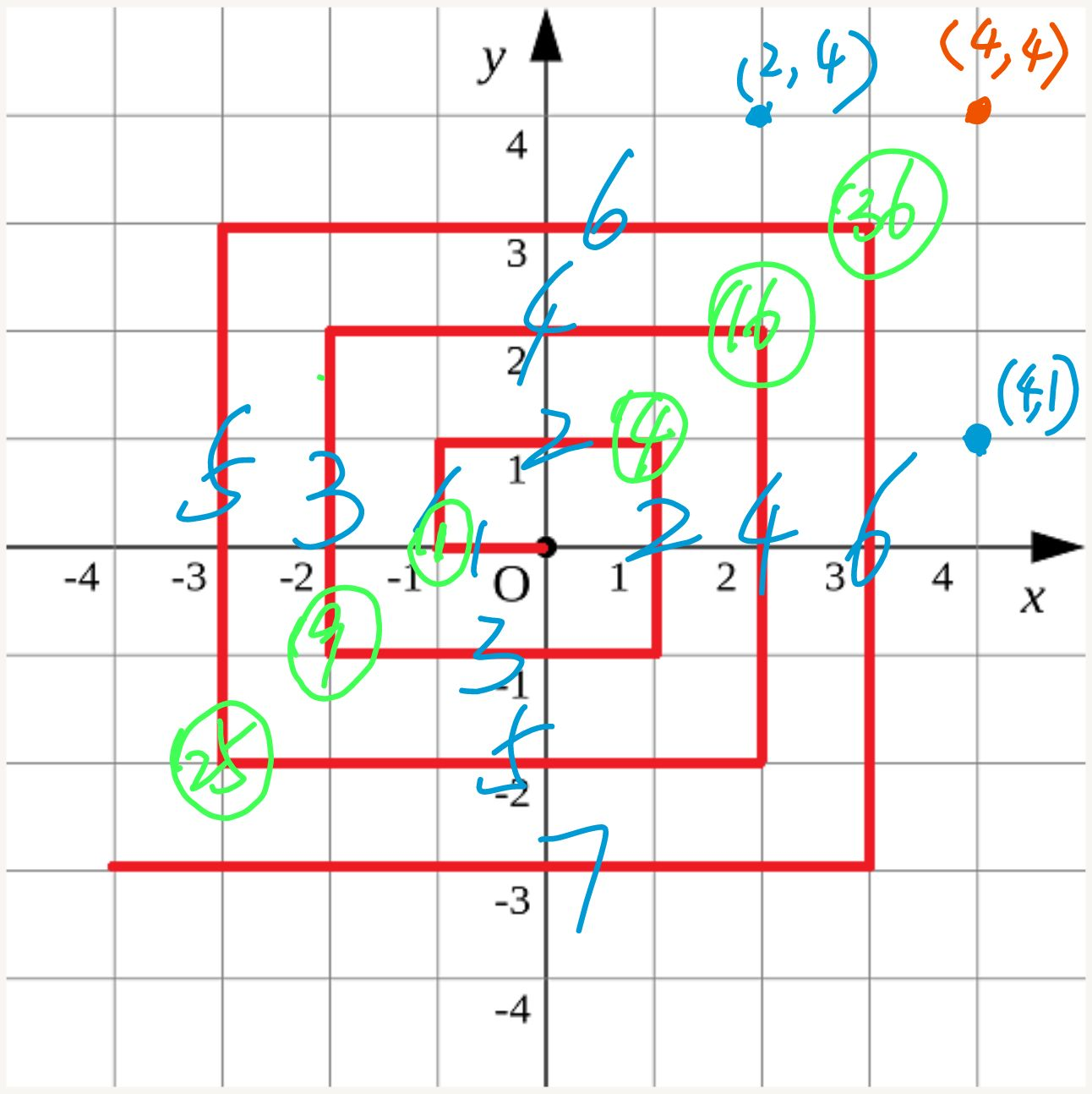
下图中，蓝色数字代表该段线段的长度，绿色圆圈数字表示从原点到该拐点的距离。另外有两个点 (2, 4) 和 (4, 1) 与拐点 (4, 4) 在同一条垂直或水平线上，可以依赖于 (4 , 4) 计算出两个点的距离。

具体思路见代码实现。

代码

#include<bits/stdc++.h>

using namespace std;

int xx, yy;
long long s;

int main() {
    cin >> xx >> yy;

    if (yy <= 0 && yy - 1 <= xx && xx <= abs(yy)) {  //下横线
        int cx = yy - 1, c = 2 * abs(yy - 1) - 1;
        s = c * 1ll * c;
        s -= xx - cx;
    } else if (xx <= -1 && xx + 1 <= yy && yy <= abs(xx)) { //左竖线
        int cy = xx + 1, c = 2 * abs(xx) - 1;
        s = c * 1ll * c;
        s += yy - cy;
    } else if (yy >= 1 && xx <= yy) { //上横线
        int cy = yy, c = yy * 2;
        s = c * 1ll * c;
        s -= cy - xx;
    } else if (xx >= 1 && yy <= xx) { //右竖线
        int cx = xx, c = xx * 2;
        s = c * 1ll * c;
        s += cx - yy;
    }

    cout << s << endl;
    return 0;
}

标题：	2018年第九届蓝桥杯省赛-G.螺旋折线
链接：	https://www.fightingok.cn/detail/207
更新：	2022-09-18 22:48:13
版权：	本文采用 CC BY-NC-SA 3.0 CN 协议进行许可