题面
6x6的方格,沿着格子的边线剪开成两部分。 要求这两部分的形状完全相同。
如下就是三种可行的分割法。
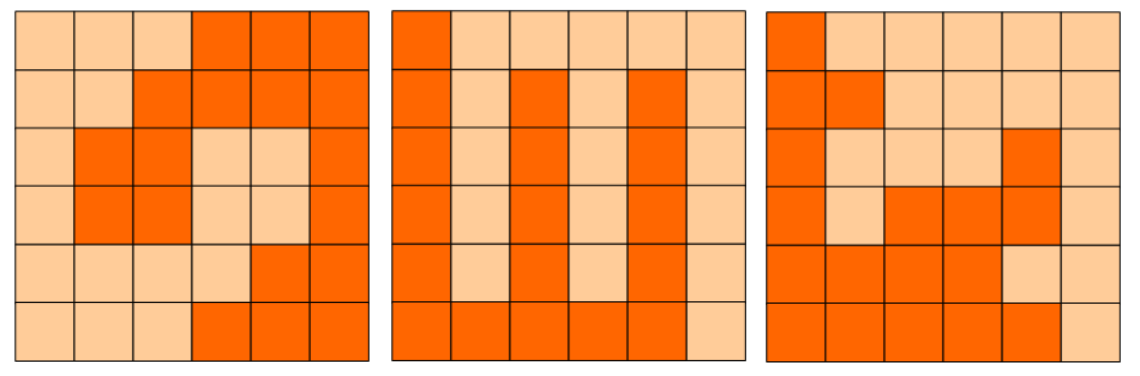
试计算: 包括这 3 种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
题解
DFS,回溯
本题可以转化思路,即为从中间点出开始,两条线按照相反方向同时向边缘进行裁剪,即可将其分为完全相同的两部分。如下图所示,从中间红色的点出发,一条沿着蓝色的线剪切,另一条沿着绿色的线进行剪切,即可得到两部分相同的图案。
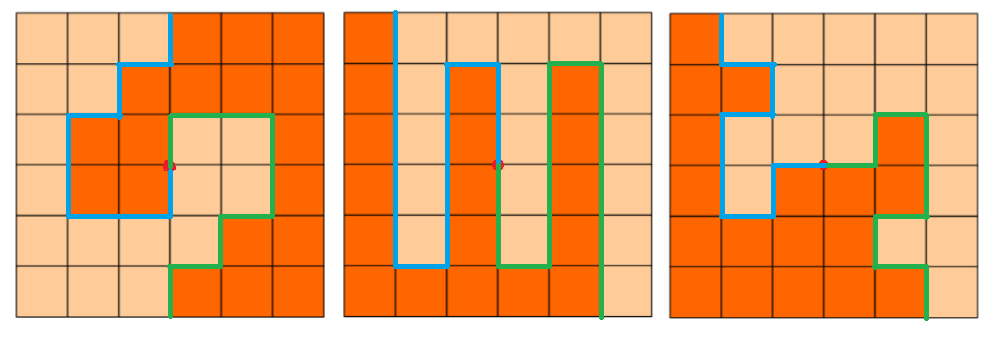
则转化为在左下角为(0,0),右上角为(6,6)中的正方形()中,以中心点(3,3)出发,走到边界的可行路线有多少条,则直接使用递归 + 回溯即可。
另,题上说旋转对称属于同一种方案,则对于4种不同方向的划分方法(经过旋转后相同),答案需要除以 4 才行。
具体见代码。
代码
#include<bits/stdc++.h>
using namespace std;
bool v[7][7];
int res, dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
void dfs(int i, int j) {
if (i == 0 || i == 6 || j == 0 || j == 6) { //到达边界即为一种合法方案
res++;
return;
}
for (int d = 0; d < 4; ++d) {
int ti = i + dir[d][0], tj = j + dir[d][1];
if (v[ti][tj]) continue;
v[ti][tj] = v[6 - ti][6 - tj] = true;
dfs(ti, tj);
v[ti][tj] = v[6 - ti][6 - tj] = false;
}
}
int main() {
v[3][3] = true;
dfs(3, 3);
cout << res / 4 << endl;
return 0;
}
| 标题: | 2017年第八届蓝桥杯省赛-D.方格分割 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/197 |
| 更新: | 2022-09-18 22:47:24 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





