题面
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
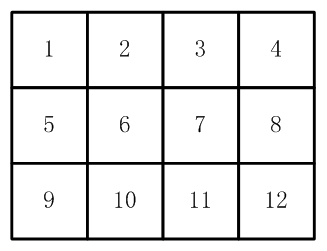
现在你要从中剪下 5 张来,要求必须是连着的。(仅仅连接一个角不算相连)
比如,【图2.jpg】,【图3.jpg】中,粉红色所示部分就是合格的剪取。
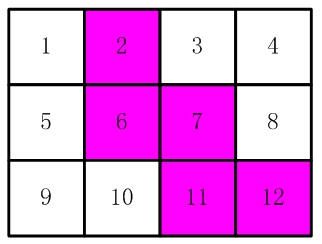
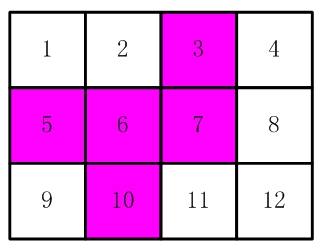
请你计算,一共有多少种不同的剪取方法。
题解
枚举,DFS,BFS
首先用 DFS 从 12 个数中选出 5 个数,将这五个数的位置用 g 数组标记起来, g[i][j] == true 代表该位置的数被选中。再用 BFS 判断这五个数是否连通即可。
答案:
116
代码
#include<bits/stdc++.h>
using namespace std;
typedef pair<int, int> PII;
int ans, dir[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
bool g[3][4], v[3][4];
bool bfs() {
memset(v, false, sizeof v);
queue<PII> q;
bool st = false;
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if (!st && g[i][j]) { //找到一个选出来的数,从它开始遍历
q.push({i, j});
v[i][j] = true;
st = true;
}
}
}
int cnt = 1;
while (q.size()) {
PII now = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int ti = now.first + dir[i][0], tj = now.second + dir[i][1];
if (ti < 0 || ti >= 3 || tj < 0 || tj >= 4) continue;
if (!g[ti][tj] || v[ti][tj]) continue;
if (++cnt == 5) return true;
q.push({ti, tj});
v[ti][tj] = true;
}
}
return false;
}
void dfs(int k, int s) {
if (s == 5) { //选出了 5 个数,进行连通性判断
if (bfs()) ans++;
return;
}
if (k == 13) return;
//该数所在坐标
int i = (k - 1) / 4;
int j = (k - 1) % 4;
//不选
dfs(k + 1, s);
//选
g[i][j] = true;
dfs(k + 1, s + 1);
g[i][j] = false; //恢复现场
}
int main() {
dfs(1, 0);
cout << ans << endl;
return 0;
}
| 标题: | 2016年第七届蓝桥杯省赛-G. 剪邮票 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/185 |
| 更新: | 2022-09-18 22:46:24 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





