题面
足球比赛具有一定程度的偶然性,弱队也有战胜强队的可能。
假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩,得出每个队与另一个队对阵时取胜的概率表:
甲 乙 丙 丁
甲 - 0.1 0.3 0.5
乙 0.9 - 0.7 0.4
丙 0.7 0.3 - 0.2
丁 0.5 0.6 0.8 -
数据含义:甲对乙的取胜概率为0.1,丙对乙的胜率为0.3,…
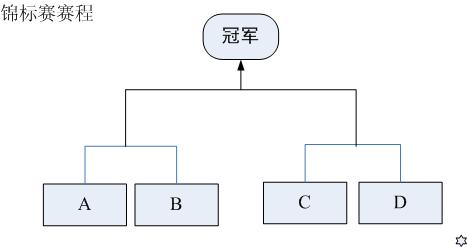
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。(参见下图)
请你进行10万次模拟,计算出甲队夺冠的概率。
题解
模拟,随机数
由题可知,要想甲获胜,有三种情况:
- 甲乙一组,丙丁一组。甲赢了乙,并赢了丙丁中获胜的一队;
- 甲丙一组,乙丁一组。甲赢了丙,并赢了乙丁中获胜的一队;
- 甲丁一组,丙乙一组。甲赢了丁,并赢了丙乙中获胜的一队。
将三种情用随机函数确定累积概率即可。
代码
#include<bits/stdc++.h>
using namespace std;
double a[4][4] = {{1, 0.1, 0.3, 0.5},
{0.9, 1, 0.7, 0.4},
{0.7, 0.3, 1, 0.2},
{0.5, 0.6, 0.8, 1}};
int main() {
double s = 0;
double p[3];
p[0] = a[0][1] * a[2][3] * a[0][2] + a[0][1] * a[3][2] * a[0][3];
p[1] = a[0][2] * a[1][3] * a[0][1] + a[0][2] * a[3][1] * a[0][3];
p[2] = a[0][3] * a[1][2] * a[0][1] + a[0][3] * a[2][1] * a[0][2];
for (int i = 0; i < 100000; i++) {
int k = rand() % 3;
s += p[k];
}
cout << s / 1000000 << endl;
return 0;
}
| 标题: | 2012年第三届蓝桥杯省赛-I.夺冠概率 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/157 |
| 更新: | 2022-09-18 22:43:51 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





