题面
【问题描述】
从一个 5x5 的方格矩阵的左上角出发,沿着方格的边走,满足以下条件的路线有多少种?
- 总长度不超过 12;
- 最后回到左上角;
- 路线不自交;
- 不走出 5x5 的方格矩阵范围之外。
如下图所示,ABC 是三种合法的路线。注意 B 和 C 由于方向不同,所以视为不同的路线。
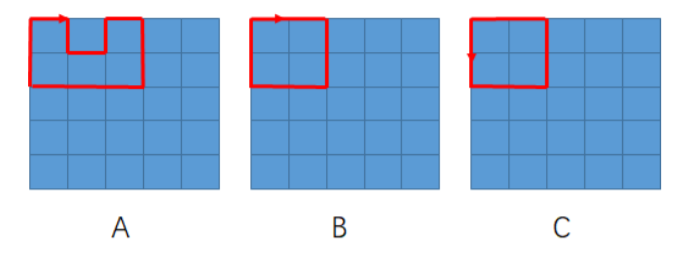
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路
暴力dfs。从起点(0,0)出发有又回到起点,走的步数小于等于12,则只要我从起点出发后能在11步以内再回到起点右边或者下面的那个点,那就算一种合法方案。
这里在每一步保存了上一步的坐标,是因为若从(0,0)出发,向右走到达(0,1),若不加判断前一步不是起点则会认为这是一种合法方案(该方案(0,0)->(0,1)->(0,0),产生自交,不合法),必须是走出去后再回到(0,1)点才行,所以记录了前一步的位置,(1,0)也同理。
答案:206
代码
#include<iostream>
using namespace std;
const int N = 10;
bool v[N][N];
int res = 0, n = 6;
int dir[4][2] = {{0, 1},
{1, 0},
{0, -1},
{-1, 0}};
void dfs(int i, int j, int pi, int pj, int s) {
//这里步数s小于等于 11 的原因是,我只要到了起点右边和下边的这两个点,那我就能走最后固定的一步到起点。
if (s <= 11 && i == 0 && j == 1 && !(pi == 0 && pj == 0)) {
//前一步不是起点(0,0),又回到(0,1)坐标,则为一种方法
res++;
return;
}
if (s <= 11 && i == 1 && j == 0 && !(pi == 0 && pj == 0)) {
//前一步不是起点(0,0),又回到(1,0)坐标,则为一种方法
res++;
return;
}
if(s == 12) return;
for (int d = 0; d < 4; d++) {
int ti = i + dir[d][0], tj = j + dir[d][1];
if (ti < 0 || ti >= n || tj < 0 || tj >= n) continue;
if (v[ti][tj]) continue;
v[ti][tj] = true;
dfs(ti, tj, i, j, s + 1);
v[ti][tj] = false;
}
}
int main() {
dfs(0, 0, -1, -1, 0);
cout << res << endl;
return 0;
}
| 标题: | 2019第十届蓝桥杯国赛-E路径计数 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/116 |
| 更新: | 2022-09-18 22:40:13 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





