题面
【问题描述】
小明要把一根木头切成两段,然后拼接成一个直角。
如下图所示,他把中间部分分成了 的小正方形,他标记了每个小正方形属于左边还是右边。然后沿两边的分界线将木头切断,将右边旋转向上后拼接在一起。
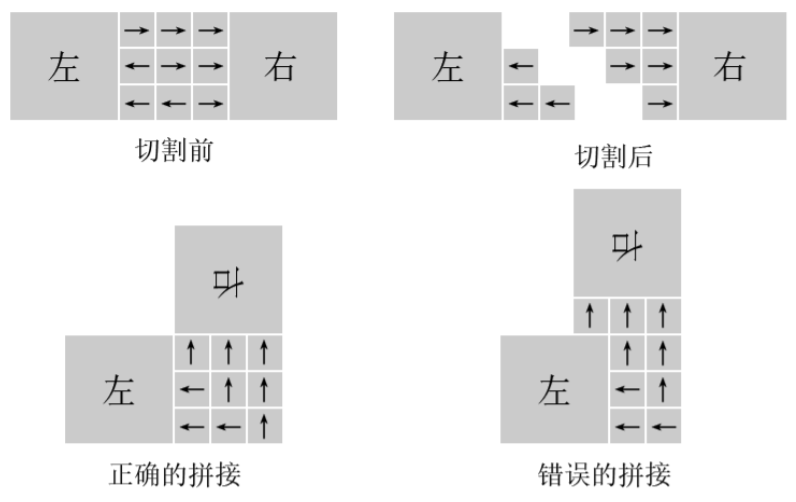
要求每个小正方形都正好属于左边或右边,而且同一边的必须是连通的。 在拼接时,拼接的部位必须保持在原来大正方形里面。
请问,对于 的小正方形,有多少种合法的划分小正方形的方式。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
思路
朴素思路,暴力枚举。(思路挺好懂,就是时间有点久,,,跑了4 min)。
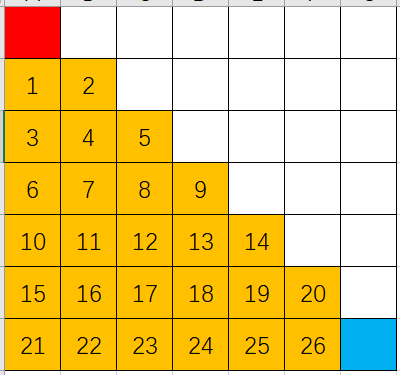
将 的矩形按照副对角线平分,枚举副对角线下面的下半部分的26个格子的选择方案(如下图)。
首先,从左上角开始,直接用位运算,用 26 位的 0 |1 二进制位,表示第几个格子选还是不选,然后再从左上角(1,1)出发bfs遍历这些格子是否为连通的路径,再从右下角(7,7)开始遍历26个格子中剩下未选择的格子是否连通,若两部分都连通则记为一种方案。
其次,上面考虑的分割方案是两部分都至少有一块木板,还有两种记为特殊的方法,就是将小木板全部分给左边的木板,或者全部分给右边的木板。
答案:2444
代码
#include<iostream>
#include<map>
#include<queue>
#include<cstring>
using namespace std;
typedef pair<int, int> PII;
int v[10][10], g[10][10];
int n, res;
int dir[4][2] = {{0, 1},
{1, 0},
{0, -1},
{-1, 0}};
map<int, PII> Map;
//bfs判断连通
int bfs(int i, int j, int k) {
int cnt = 1;
queue<PII> q;
q.push(make_pair(i, j));
v[i][j] = true;
while (q.size()) {
PII now = q.front();
q.pop();
for (int d = 0; d < 4; d++) {
int ti = now.first + dir[d][0], tj = now.second + dir[d][1];
if (ti < 1 || ti > n || tj < 1 || tj > n || ti < tj) continue;
if (v[ti][tj]) continue;
if (g[ti][tj] != k) continue;
v[ti][tj] = true;
cnt++;
q.push(make_pair(ti, tj));
}
}
return cnt;
}
int main() {
while (cin >> n) {
res = 0;
int s = n * (n + 1) / 2 - 2;
int k = 0;
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i; j++) {
Map[k] = make_pair(i, j);
k++;
}
}
for (int i = 0; i < 1 << s; i++) {
memset(v, false, sizeof v);
for (int x = 1; x <= n; x++) {
for (int y = 1; y <= x; y++) {
g[x][y] = 2;
}
}
g[1][1] = 1;
int t = 1;
for (int j = 0; j < s; j++) {
if (i >> j & 1) {
g[Map[j].first][Map[j].second] = 1;
t++;
}
}
int cnt;
if (t < s + 2 - t) {
cnt = bfs(1, 1, 1);
if (cnt < t) continue;
cnt += bfs(n, n, 2);
} else {
cnt = bfs(n, n, 2);
if (cnt < s + 2 - t) continue;
cnt += bfs(1, 1, 1);
}
if (cnt == s + 2) res++;
}
cout << res + 2 << endl; //加上特殊情况
}
return 0;
}
| 标题: | 2019第十届蓝桥杯国赛-C拼接 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/114 |
| 更新: | 2022-09-18 22:40:03 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





