题面
【问题描述】
皮亚诺曲线是一条平面内的曲线。
下图给出了皮亚诺曲线的 1 阶情形,它是从左下角出发,经过一个 3 × 3 的 方格中的每一个格子,最终到达右上角的一条曲线。
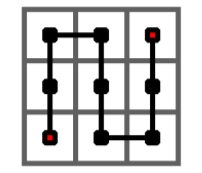
下图给出了皮亚诺曲线的 2 阶情形,它是经过一个 的方格中的每一个格子的一条曲线。它是将 1 阶曲线的每个方格由 1 阶曲线替换而成。
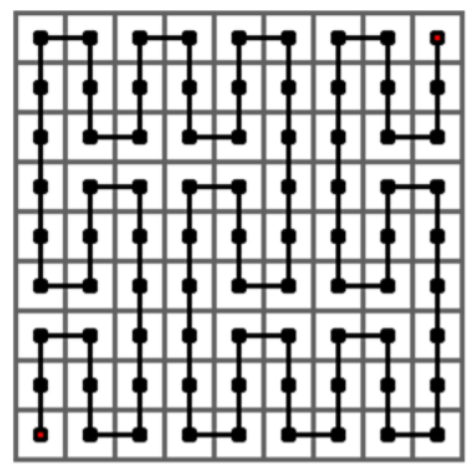
下图给出了皮亚诺曲线的 3 阶情形,它是经过一个 的方格中的每一个格子的一条曲线。它是将 2 阶曲线的每个方格由 1 阶曲线替换而成。

皮亚诺曲线总是从左下角开始出发,最终到达右上角。
我们将这些格子放到坐标系中,对于 k 阶皮亚诺曲线,左下角的坐标是 ,右上角坐标是 ,右下角坐标是 ,左上角坐标是 。
给定 k 阶皮亚诺曲线上的两个点的坐标,请问这两个点之间,如果沿着皮亚诺曲线走,距离是多少?
【输入格式】
输入的第一行包含一个正整数 k,皮亚诺曲线的阶数。
第二行包含两个整数 x1, y1,表示第一个点的坐标。
第三行包含两个整数 x2, y2,表示第二个点的坐标。
【输出格式】
输出一个整数,表示给定的两个点之间的距离。
【样例输入1】
1
0 0
2 2
【样例输出1】
8
【样例输入2】
2
0 3
0 3
【样例输出2】
13
【评测用例规模与约定】
对于 30% 的评测用例,0 ≤ k ≤ 10。
对于 50% 的评测用例,0 ≤ k ≤ 20。
对于所有评测用例,0 ≤ k ≤ 100, 0 ≤ x1, y1, x2, y2 < , x1, y1, x2, y2 ≤ 。 数据保证答案不超过 。
思路
- 已经通过所有样例,仅供参考
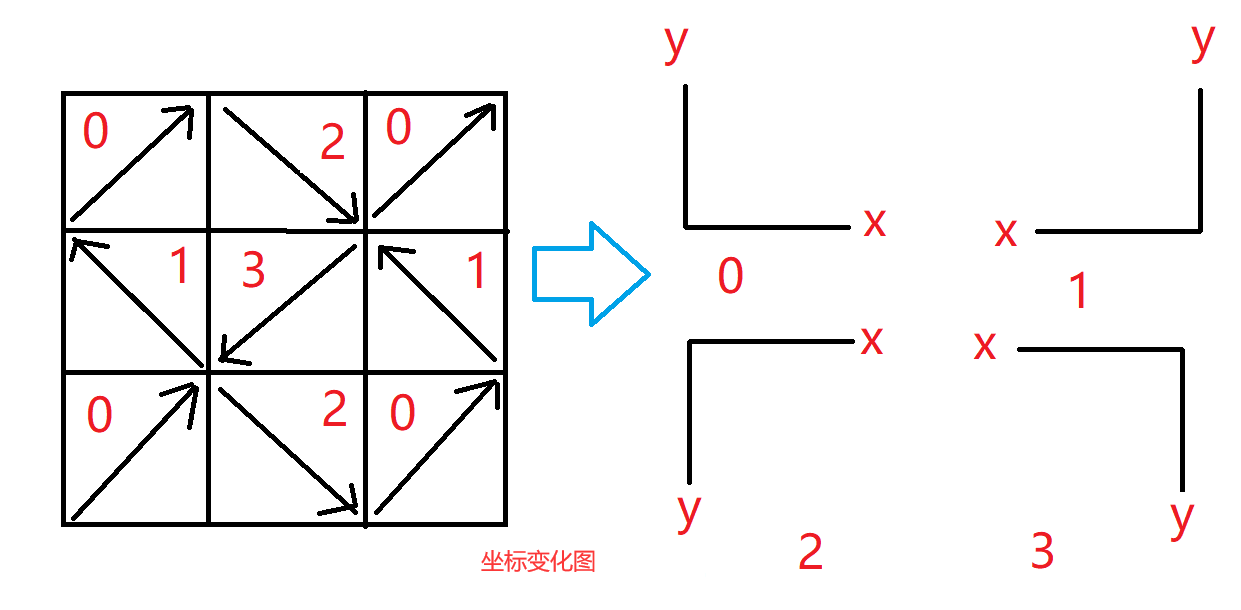
分形题,注意每个 格子的坐标的翻转、旋转和对称等情况,再使用递归即可,见下图的坐标转换图,具体实现参考代码。
注意:
- 在数据量 k >= 40 后,会爆longlong,直接舍掉取 39 就能正确(不知道为啥,挺离谱的。。。)。
- 其中的求幂运算为浮点运算,在数据量过大时会失真,需自己编写快速幂来求整数次幂。
代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL qpow(LL a, int n) {
LL s = 1;
while (n) {
if (n & 1) s *= a;
a *= a;
n >>= 1;
}
return s;
}
LL calc(int n, LL x, LL y) {
if (n == 0) return 0;
if (n > 1) {
LL size = qpow(3LL, n - 1); //边长
LL cnt = size * 1LL * size; //面积
LL dx = x / size, dy = y / size;
LL k;
if (dx == 0 || dx == 2) k = dx * 3 + dy;
else k = 5 - dy;
LL out_size = k * cnt; //当前外部的距离
LL tx = x % size, ty = y % size;
if (k == 1 || k == 7) tx = size - 1 - tx;
if (k == 3 || k == 5) ty = size - 1 - ty;
if (k == 4) {
tx = size - 1 - tx;
ty = size - 1 - ty;
}
return calc(n - 1, tx, ty) + out_size;
}
if (x == 0 || x == 2) return x * 3 + y;
return 5 - y;
}
int main() {
int k;
LL x1, y1, x2, y2;
cin >> k;
cin >> x1 >> y1;
cin >> x2 >> y2;
if (k >= 40) k = 39; //3^40爆long long
LL idx1 = calc(k, x1, y1);
LL idx2 = calc(k, x2, y2);
printf("%lld\n", abs(idx1 - idx2));
return 0;
}
| 标题: | 2020第十一届蓝桥杯国赛-F皮亚诺曲线距离 |
|---|---|
| 链接: | https://www.fightingok.cn/detail/109 |
| 更新: | 2022-09-18 22:39:35 |
| 版权: | 本文采用 CC BY-NC-SA 3.0 CN 协议进行许可 |





